常数项级数的概念和性质

---

级数及其收敛性概念

(1)给定一个数列u₁，u₂，…，u_n，…，则表达式u₁+u₂+…+u_n+…

叫做无穷级数简称级数．记作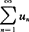，即

u_n叫做级数的一般项．

(2)收敛、发散的定义

S_n=u₁+u₂+…+u_n

叫做级数的部分和．

如果limS_n存在，则称级数收敛且其极限叫做级数的和，并记为

否则称级数发散．

收敛级数的基本性质

(1)如果级数收敛于和S，则它的每项同乘以一个与项n无关的常数k所得的级数也收敛，且其和为kS，即

(2)设级数及分别收敛于和S及σ，则级数也收敛，且其和为S±σ，即

(3)若级数中去掉、加上或改变有限项的值，则不改变级数的收敛性．

(4)如果级数收敛，则对该级数的项任意加括号后所成的级数

(u₁+…+u_n1)+(u_n1+₁+…+u_n2)+…+(u_nk－1+…+u_nk)+…仍收敛，且其和不变．

(5)若级数收敛，则．其逆不真．

柯西审敛原理 级数收敛的充分必要条件为：对于任意给定的正数ε，总存在相应的正整数N，当n＞N时，对于任意自然数p，恒有

|u_n+1+u_n+2+…+u_n+p|＜ε．