向量的内积

---

向量的内积 设n维向量α=(a₁，a₂，…，a_n)，β=(b₁，b₂，…，b_n)．则α，β的内积记作(α，β)，且定义为

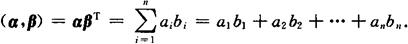
内积的性质

(1)对称性：(α，β)=(β，α)．

(2)线性性：(α+β，γ)=(α，γ)+(β，γ)；(kα，β)=(α，kβ)=k(α，β)．

(3)正定性：(α，α)≥0，当且仅当α=0时，等号成立．

向量的长度

向量α的长度记作‖α‖，且定义为

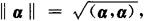
显然．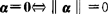

两向量间的夹角

两向量α，β之间的夹角记作〈α，β〉，且定义为

即

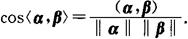
显然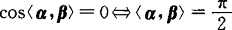(称为向量α，β正交)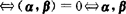相互正交．

柯西－施瓦茨(Cauchy-Schwarz)不等式

|(α，β)|≤‖α‖‖β‖．

三角形不等式

‖α+β‖≤‖α‖+‖β‖．

欧氏空间

定义了内积运算的实n维向量空间称为n维欧几里得空间(简称欧氏空间)，仍记作Rn．