单相正弦交流电路

---

1．纯电阻电路

图2－40为纯电阻电路及其相量图。

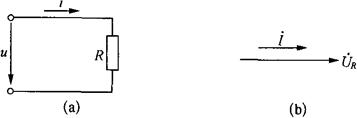
图2—40 纯电阻电路及其相量图

(1)电流与电压的关系

瞬时值表达式为：

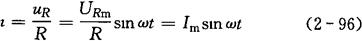
最大值表达式为：

式中 U_Rm——负载两端电压的最大值(V)；

I_m——电路中电流的最大值(A)。

有效值表达式为：

式中 U_R——负载两端电压的有效值(V)；

I——电路中电流的有效值(A)。

相量表达式为：

式中 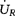——负载两端电压的复量(V)；

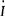——电路中电流的复量(A)。

上述各式表明、电流与电压的频率相同；电流与电压的相位相同，如图2－40(b)所示；电流与电压的数量关系仍符合欧姆定律。

(2)电功率及电能的计算

瞬时功率：

p_R=u_R·i=U_RI－UIcos2ωt (2－100)

有功功率：

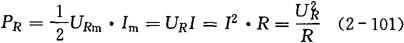
电能：

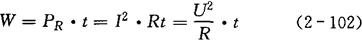
式中 p_R——瞬时功率(W)，瞬时功率是恒定分量U_RI和交变分量之和；

P_R——有功功率(W)，有功功率等于最大瞬时功率的一半；

W——电能(J)。

［例2－30］ 已知一白炽灯工作时的电阻为484Ω，其两端加有的正弦电压为u=311sin314t(V)，试求：①电流有效值，并写出电流瞬时值解析式；②白炽灯的有功功率。

［解］ ①由u=311sin314t(V)可知，正弦电压的有效值为

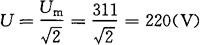
则正弦电流的有效值为

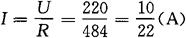
又因白炽灯可视为纯电阻，电流与电压同相，所以正弦电流瞬时值的解析式为

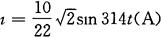
②由有功率公式可求白炽灯的有功功率为

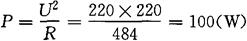
2．纯电感电路

图2－41为纯电感电路及其相量图。

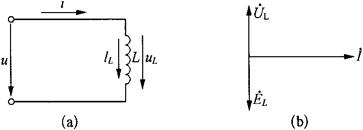
图2－41 纯电感电路及相量图

(1)电流与电压的关系

瞬时值表达式为：

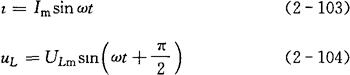
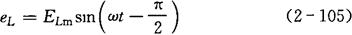
最大值表达式为：

式中 X_L——感抗，X_L=ωL=2πfL(Ω)。

有效值表达式为：

相量表达式为：

纯电感电路中，电流与电压频率相同；相位上，电压超前电流90°，自感电动势滞后电流90°，如图2－41(b)所示；电流与电压的有效值或最大值之间的数量关系符合欧姆定律。由于电流与电压的相位不同，所以电流与电压的瞬时值之间的数量关系不符合欧姆定律，即感抗X_L只代表电流与电压的有效值或最大值的比值，而不代表电流与电压的瞬时值的比值。

对直流电来说，由于f=0，则X_L=0，即电感L对直流电没有阻碍作用。

(2)电功率及磁场能的计算

瞬时功率：

P_L=U_L·Isin2ωt (2－109)

有功功率：

P_L=0 (2－110)

无功功率

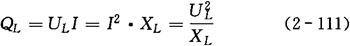
磁场能

式中 Q——无功功率(W)，必须指出，“无功”的含义是“交换”而不是“消耗”，它是相对“有功”而言的，决不能理解“无用”。具有电感性质的变压器，电动机等设备都是靠电磁转换工作的，因此，若无功率，这些设备就无法工作；

W_L——磁场能(J)。

［例2－31］ 设有一电阻可以忽略的线圈接在正弦交流电源上，已知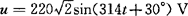，线圈的电感量L=0．7H。

求：①写出流过线圈的电流的瞬时值表达式；②电路的无功功率；③作电流和电压的相量图。

［解］ ①流过线圈的电流的瞬时值表达式为：

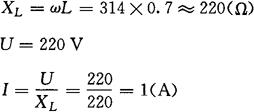
φ_u=30°，又电流滞后电压90°，所以

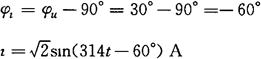
②无功功率

Q_L=U·I=220×1

=220(W)

③电流和电压的相量图如图2－42所示。

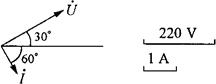
图2－42

3．纯电容电路

图2－43为纯电容电路及相量图。

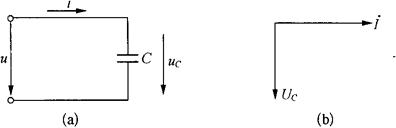
图2－43 纯电容电路及相量图

(1)电流与电压的关系

瞬时值表达式为：

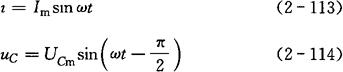
最大值表达式为：

式中 XC——容抗，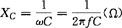

有效值表达式为：

相量表达式为：

纯电容电路中，电流与电压频率相同，相位上，电压滞后电流90°，如图2－43(b)所示；电流与电压的有效值或最大值之间的数量关系符合欧姆定律。由于电流与电压的相位不同，所以电流与电压的瞬时值之间的数量关系不符合欧姆定律，即容抗X_C只代表电流与电压的有效值或最大值的比值，而不代表电流与电压的瞬时值的比值。

对直流电来说，由于f=0，则X_C=∞，即电容C具有隔直流的作用。

(2)电功率和电场能的计算

瞬时功率：

p_C=U_CIsin2ωt (2－119)

有功功率：

P_C=0 (2－120)

无功功率：

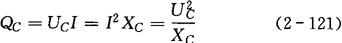
电场能：

式中 W_C——电场能(J)。

［例2－32］ 已知某电容电路两端所加的正弦交流电压为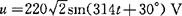，电容量C=20μF，求：①写出流过电容的电流的瞬时值表达式；②电路的无功功率；③作电流和电压的相量图。

［解］ ①流过电容的电流的瞬时值表达式为：

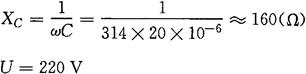
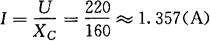
φ_u=30°，又电流超前电压90°，所以

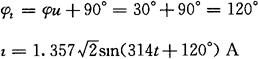
②无功功率

Q_C=UI=220×1．375≈303(W)

③电流和电压的相量图如图2－44所示。

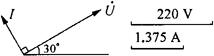
图2－44

4．电阻、电感、电容串联的正弦交流电路

图2－45是R、L、C串联的正弦交流电路。

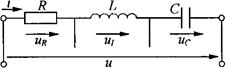
图2－45 R、L、C串联的正弦交流电路

(1)电流与电压的关系

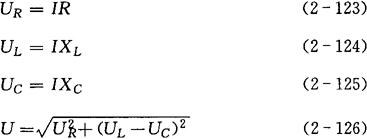
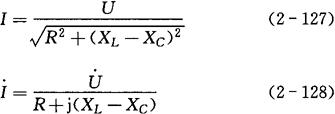
(2)复数阻抗的计算

Z=R+_j(X_L－X_C) (2－129)

模：

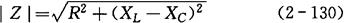
阻抗角(电压与电流的相位差)：

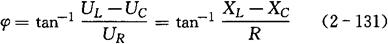
φ角的大小与正负取决于X_L、X_C与R的数值。下面分三种情况说明：

①当X_L＞X_C时，tanφ＞0，φ＞0，总电压U超前电流I，电路呈感性。

②当X_L＜X_C时，tanφ＜0，φ＜0，总电压U滞后电流I，电路呈容性。

③当X_L=X_C时，tanφ=0，φ=0，总电压U与电流I同相，电路呈阻性。

(3)电功率的计算

瞬时功率：

p=UICosφ－UIcos(2ωt+φ) (2－132)

有功功率：

P=UIcosφ=U_R·I=I²·R (2－133)

无功功率：

Q=UIsinφ=I(U_L－U_C)=I²(X_L－X_C) (2－134)

视在功率：

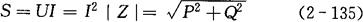
式中 S——视在功率(W)。

［例2－33］ 在图2－45中，已知R=2Ω，L=160mH，C=66μF，加在电路两端的交流电压的有效值U=220V，频率f=400Hz。求①电路的阻抗；②电路的电流；③各元件两端的电压；④电路的P、Q、S；⑤电路的性质。

［解］ ①电路的阻抗

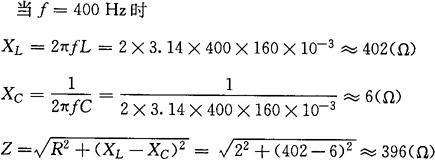
②电路的电流

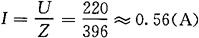
③电阻R、电感L及电容C上的电压

U_R=I·R=0．56×2=1．12(V)

U_L=IX_L=0．56×402=225．12(V)

U_C=I·X_C=0．56×6=3．36(V)

④电路的有功功率P、无功功率Q及视在功率S

P=U_R·I=1．12×0．56≈0．63(W)

Q=(U_L－U_C)·I=(225．12－3．36)×0．56

≈124．19(W)

S=UI=220×0．56=123．2(W)

⑤电路的性质

因为：

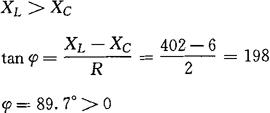
所以电路呈感性。

［例2－34］ 已知电阻R=30Ω，电感L=382mH，电容C=40μF组成的串联电路，接于电源电压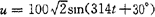V的电源两端。用相量法求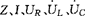，并画相量图。

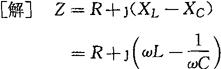
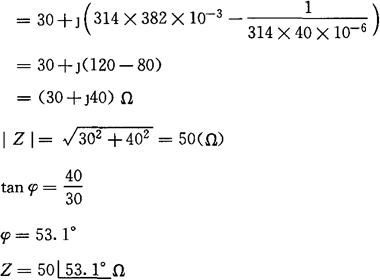
由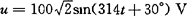得

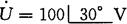
则

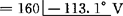
相量图如图2－46所示。

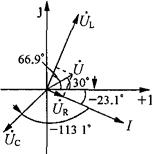
图2－46 例2－34的相量图

5．电阻、电感、电容并联的正弦交流电路

图2－47是R、L、C并联的正弦交流电路。

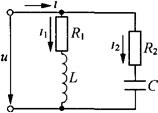
图2－47 R、L、C并联的正弦交流电路

(1)电流和电压的计算

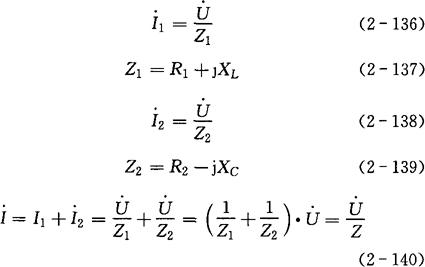
式中 Z——并联电路的等效复阻抗。

Z与Z₁、Z₂的关系为：

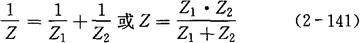
对于有n条支路并联的电路，其等效复阻抗Z与各支路复阻抗的关系为：

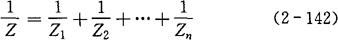
(2)复导纳的计算

复数阻抗的倒数叫复导纳，用符号Y表示，其数学表达式为：

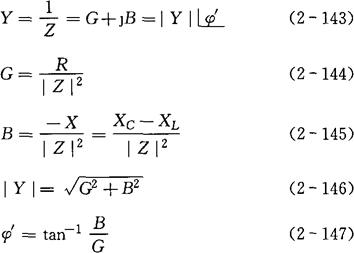
式中 Y——复导纳(西门子，用符号S表示)；

R——电阻(Ω)；

Z——复阻抗(Ω)；

｜Z｜——复阻抗的模(Ω)；

G——电导，即复导纳Y的实部(S)；

B——电纳，即复导纳Y的虚部(S)；

X——电抗(Ω)；

X_L——感抗(Ω)；

X_C——容抗(Ω)；

｜Y｜——复导纳的模(S)；

φ′——导纳角，即复导纳Y的辐角。

将复导纳与复阻抗对比

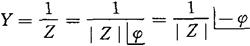
复导纳的模等于对应复阻抗模的倒数，即：

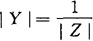
导纳角等于对应阻抗角的负值，即：

φ′=－φ

(3)电功率的计算

同R、L、C串联正弦交流电路电功率的计算。

［例2－35］ 在图2－47中，已知R₁=30Ω，R₂=8Ω，X_L=40Ω，X_C=6Ω，电源电压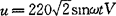，求该电路的分支电流I₁、I₂和总电流I，并作相量图。

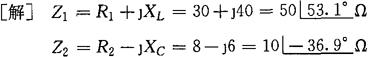
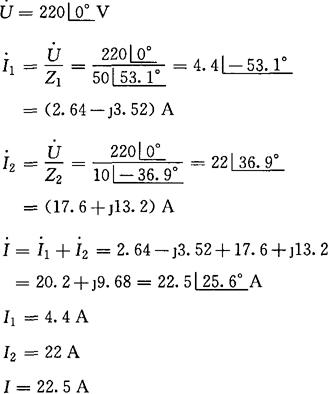
相量图如图2－48所示。

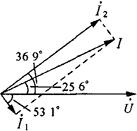
图2－48

［例2－36］ 在图2－49中，已知u=424sin5000tV，R₁= 10Ω，R₂=13Ω，R₃=2Ω，C=20μF，L=4mH，求总电流i及电压u_cb。

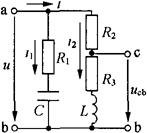
图2－49

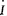超前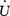说明整个电路呈容性。

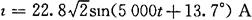
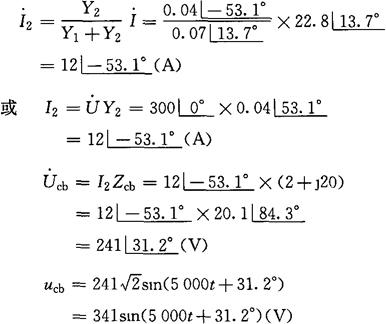
6．谐振电路

在具有电感和电容的电路中，如果电流和电压达到同相位，则电路会产生谐振现象，处于谐振状态的电路称为谐振电路。

(1)串联谐振

在R、L、C串联电路中，当X_L=X_C时，电流与电压同相位，这种现象称为串联谐振。

①谐振条件。

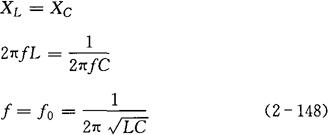
式中 f——电源频率(Hz)；

f₀——谐振频率，又称电路的固有频率(Hz)。谐振频率取决于电路参数L与C的数值，若L与C为定值时，调节电源频率使它与电路的固有频率相等，电路就发生谐振。反之若电源频率一定时，调节L和C的大小，使电路的固有频率等于电源频率时，电路也能发生谐振。收音机的输入调谐电路，就是通过改变C的大小，来选不同频率的广播电台的串联谐振电路。

②串联谐振电路具有的特点。

a．串联谐振时，电路的阻抗最小，且呈阻性。此时电路中的电流为最大。

串联谐振阻抗为：

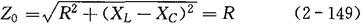
串联谐振时的电流为：

b．串联谐振时，电感两端电压U_L与电容两端电压U_C数值相等，且数值可以比总电压大许多倍。

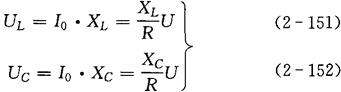
式中，X_L／R、X_C／R分别为U_L、U_C与U的比值，这个比值称为谐振电路的品质因数，用符号Q表示，即：

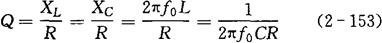
因此

U_L=U_C=QU (2－154)

即串联谐振时，电感、电容两端的电压为总电压的Q倍。一般串联谐振电路中的R很小，所以Q值总大于1。由于串联谐振会在电感、电容上产生高电压，所以串联谐振又称为电压谐振。

串联谐振用于微弱信号的放大，但电力工程由于电源电压本身很高，所以应避免产生电压谐振。

③谐振时，电功率的计算。

无功功率：

Q_L=Q_C，Q=0 (2－155)

有功功率：

P=I²R (2－156)

视在功率：

S=P (2－157)

［例2－37］ 已知R、L、C串联电路中的L=30μH，C=211pF，R=9．4Ω，电源电压U=100μV。若电路产生串联谐振，求谐振频率f₀，品质因数Q及电容两端的电压U_C。

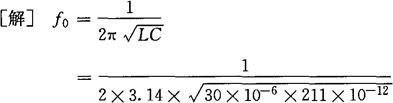
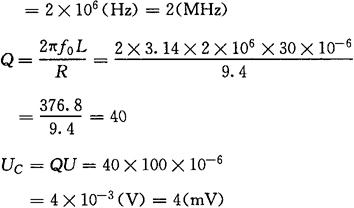
(2)并联谐振

L与C并联时，若I_LY=I_C，(I_LY为I_L在Y方向的分量)，则总电流与电压同相，这种现象称为并联谐振。

①谐振条件。一般电感线圈的电阻通常很小，可以忽略，这时并联谐振的条件是：

X_L=X_C

谐振频率为：

②并联谐振电路具有的特点。

a．并联谐振时，因总电流最小，所以电路的阻抗为最大，且呈阻性。即

I₀=QX_L=QX_C

式中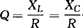——电路的品质因数。

上式表明，并联谐振时，电路的阻抗为感抗或容抗的Q倍。

b．并联谐振时，电感支路和电容支路的电流大小近似相等，方向近似相反，且为总电流的Q倍。即

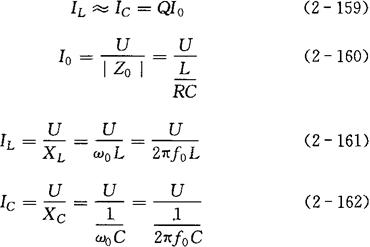
③谐振时电功率的计算。与串联谐振电路相同。

并联谐振电路主要用于振荡器和选频器，收音机、电视机的“中周”就是并联谐振电路。

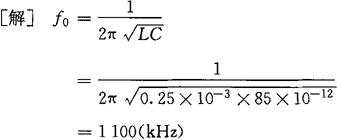
［例2－38］ 电阻R与电感L串联后再与电容C并联的电路中，已知R=25Ω，L=0．25mH，C=85pF。求电路的谐振频率f₀，品质因数Q和谐振时电路的阻抗模｜Z₀｜。

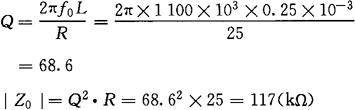
7．复杂正弦交流电路的计算

复杂正弦交流电路的计算和直流电路所用的定理、定律及计算电路的方法一样，所不同的是电压和电流以相量表示，电阻、电感、电容及其组成的电路以复数阻抗或复数导纳来表示。

(1)网孔电流表

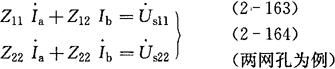
［例2－39］ 图2－50所示电路中，已知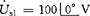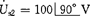， ，R=5Ω，X_L=5Ω，X_C=2Ω，求各支路电流。

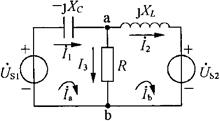
图2－50 正弦交流电路的网孔电流法

［解］ 选定支路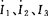电流和网孔电流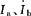的参考方向如图所示。

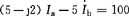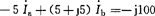选绕行方向与网孔电流参考方向一致，列出网孔方程 (1) (2)

由式(1)得

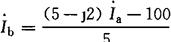
代入(2)式得

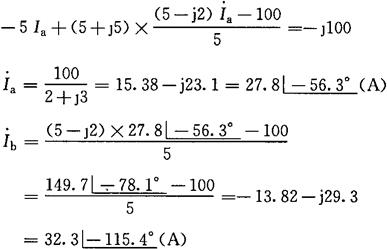
各支路电流

所以

I₁=27．8A，I₂=32．3A，I₃=29．9A

(2)节点电压法 (2－165)

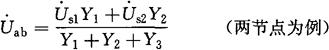
［例2－40］ 图2－50所示电路中，已知数据同例2－39，试用节点法求各支路电流。

［解］ 设支路电流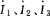的参考方向如图所示，并以b点为参考点。

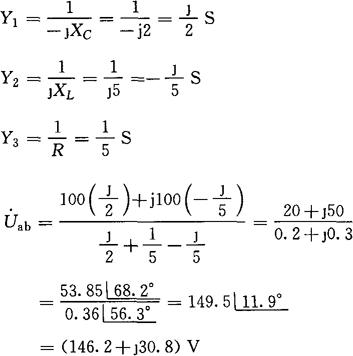
各支路电流

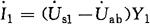
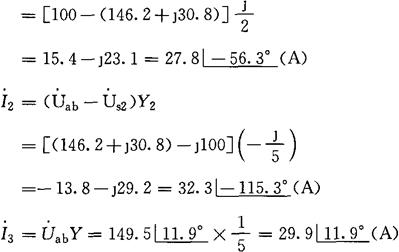
所以

I₁=27．8A，I₂=32．3A，I₃=29．9A

(3)戴维南定理求解

对于图2－50所示电路，用戴维南定理求R支路的电流，方法如下：

将电路进行整理，整理后的电路可看作由虚线框内含原二端网络和R支路所组成，如图2－51(a)所示。

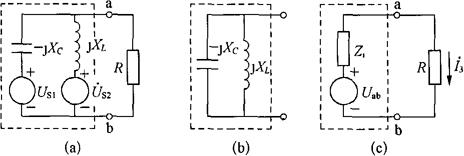
图2－51 对图2－50电路的整理

先求开路电压，即将R支路断开后a、b两点间的电压。即：

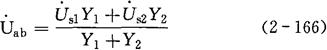
再求入端阻抗(见图2－51(b))，即：

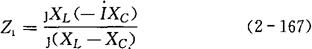
虚框内含源二端网络的等效电路如图2－51(c)所示，这样R中的电流为：

［例2－41］ 试用戴维南定理求图2－51(a)电路中R支路的电流。已知条件同例2－39。

［解］ 选定支路电流的参考方向同前。先求开路电压，即：

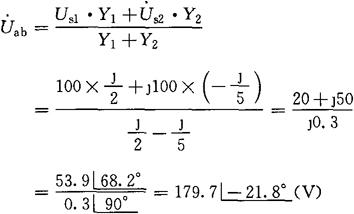
再求入端阻抗，即：

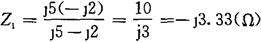
R中的电流为：

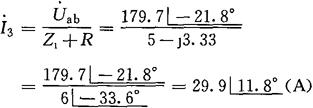
所以

I₃=29．9(A)