函数展开为幂级数的方法
直接法 首先求出f(x)在x0处的各阶导数，其次计算泰勒公式中的余项
(ξ在x0与x之间)在x的什么区域上趋向于0(当n→∞时)．
间接法 利用一些已知函数的幂级数的展开式、幂级数的运算(如四则运算，逐项微分法，逐项积分法)以及变量代换法，将所给函数展开为幂级数．
例1 将
展开为麦克劳林级数．
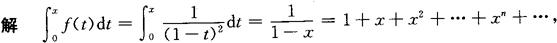
逐项求导，得f(x)的麦克劳林级数
例2 将e－x2展开为麦克劳林级数．
解 因为
将x用－x2代入，得e－x2的麦克劳林级数，为
欧拉公式
eix=cosx+isinx，
由此可得
- 绵海海儿是什么意思
- 绵渺是什么意思
- 绵炭是什么意思
- 绵爪爪儿是什么意思
- 绵瓜子相似是什么意思
- 绵甜是什么意思
- 绵甲是什么意思
- 绵白糖是什么意思
- 绵皋是什么意思
- 绵皮树是什么意思
- 绵盘是什么意思
- 绵眇是什么意思
- 绵着是什么意思
- 绵矩是什么意思
- 绵石栎是什么意思
- 绵秤是什么意思
- 绵稍是什么意思
- 绵竹是什么意思
- 绵竹、广汉之战是什么意思
- 绵竹东方工业开发区是什么意思
- 绵竹中学是什么意思
- 绵竹关是什么意思
- 绵竹剑南春是什么意思
- 绵竹县是什么意思
- 绵竹县乡土志是什么意思
- 绵竹县志是什么意思
- 绵竹县特殊教育中心是什么意思
- 绵竹市（剑南镇）是什么意思
- 绵竹年画是什么意思
- 绵竹木版年画是什么意思
- 绵竹杨先生事略是什么意思
- 绵竹起义是什么意思
- 绵笃是什么意思
- 绵精是什么意思
- 绵紬是什么意思
- 绵絮头是什么意思
- 绵絮头草是什么意思
- 绵纩是什么意思
- 绵纱是什么意思
- 绵纸是什么意思
- 绵络是什么意思
- 绵绣是什么意思
- 绵续是什么意思
- 绵绳套索是什么意思
- 绵绵是什么意思
- 绵绵不休是什么意思
- 绵绵不已是什么意思
- 绵绵不息是什么意思
- 绵绵不断是什么意思
- 绵绵不绝是什么意思
- 绵绵不绝，必有乱结；纤纤不伐，必成妖孽是什么意思
- 绵绵不绝，缦缦奈何？毫毛不拔，将成斧柯是什么意思
- 绵绵不绝，蔓蔓奈何是什么意思
- 绵绵善善是什么意思
- 绵绵土是什么意思
- 绵绵密密是什么意思
- 绵绵无穷事，各各驰绕身。是什么意思
- 绵绵早晚休。是什么意思
- 绵绵此恨是什么意思
- 绵绵瓜瓞是什么意思