二重积分的换元法
二重积分的换元法 设f(x,y)在Oxy平面上的闭区域D上连续.变换

(1)x(u,v),y(u,v)在D′具有一阶连续偏导数,
(2)在D′上雅可比(Jacobi)行列式
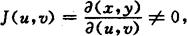
其中
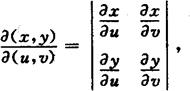
(3)变换T:D′→D是一对一的,则有

上式称为二重积分的换元公式.
注 雅可比式J(u,v)只在D′上个别点或一条曲线上为零,公式仍成立.
例  ,其中D是x≥0,y≥0及
,其中D是x≥0,y≥0及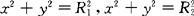 (R1<R2)如图10.6所示的闭区域.
(R1<R2)如图10.6所示的闭区域.
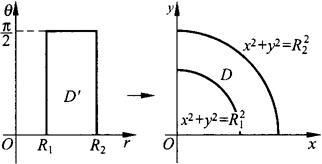
图10.6
解 做变换T
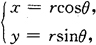
将D′:r=R1,r=R2,θ=0及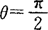 变换为D,而雅可比式为
变换为D,而雅可比式为
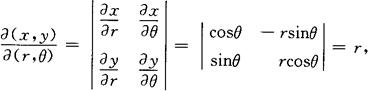
则
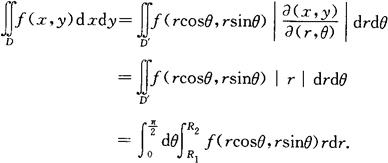
- 诡辩(论)是什么意思
- 诡逸是什么意思
- 诡遇是什么意思
- 诡道是什么意思
- 诡道可使由之,不可使知之是什么意思
- 诡避是什么意思
- 诡错是什么意思
- 诡问是什么意思
- 诡间是什么意思
- 诡险是什么意思
- 诡随是什么意思
- 诡随嫌弱操,羁束谢贞肥。是什么意思
- 诡雅异俗是什么意思
- 诡雷是什么意思
- 诡靡是什么意思
- 诡饰是什么意思
- 诡駮是什么意思
- 诡驳是什么意思
- 诡髻是什么意思
- 诡黠是什么意思
- 询是什么意思
- 询事考言是什么意思
- 询事考言,循名责实。是什么意思
- 询于刍荛是什么意思
- 询于四岳。是什么意思
- 询于芻荛是什么意思
- 询五是什么意思
- 询价是什么意思
- 询价信是什么意思
- 询价函是什么意思
- 询价单是什么意思
- 询价采购是什么意思
- 询刍录是什么意思
- 询叩是什么意思
- 询叫是什么意思
- 询呃是什么意思
- 询咨是什么意思
- 询商之辞是什么意思
- 询喉是什么意思
- 询复是什么意思
- 询审是什么意思
- 询家是什么意思
- 询察是什么意思
- 询局是什么意思
- 询局的是什么意思
- 询查是什么意思
- 询根问底是什么意思
- 询求是什么意思
- 询求,访求是什么意思
- 询监是什么意思
- 询盘是什么意思
- 询直是什么意思
- 询租是什么意思
- 询究是什么意思
- 询索是什么意思
- 询纳是什么意思
- 询考是什么意思
- 询芻是什么意思
- 询荛是什么意思
- 询訏之乐是什么意思