二维随机变量的联合分布

---

设随机试验E，样本空间Ω=｛e｝，X(e)，Y(e)是定义在Ω上的两个随机变量，它们构成随机向量(X，Y)，叫做二维随机变量．

联合分布函数

1．定义

设二维随机变量(X，Y)．对变量x，y，二元函数

F(x，y)=P｛X≤x，Y≤y｝

称为(X，Y)的联合分布函数，简称分布函数．

2．分布函数的性质

(1)0≤F(x，y)≤1；

(2)F(x，y)对x，y分别是单调非降的，即对任意的y，若x₁＜x₂，则F(x₁，y)≤F(x₂，y)；对任意的x，若y₁＜y₂，则有F(x，y₁)≤F(x，y₂)；

(3)对任意的x，y，有F(x，－∞)=0，F(－∞，y)=0，并且有F(－∞，－∞)=0，F(+∞，+∞)=1．

(4)对任意x(或y)，F(x，y)是右连续的，即

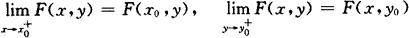
(5)对任意的x₁＜x₂，y₁＜y₂，有

F(x₂，y₂)－F(x₁，y₂)－F(x₂，y₁)+F(x₁，y₁)≥0．

离散型随机变量的联合分布律

若随机变量(X，Y)的所有取值为有限对或无限可列多对，则称(X，Y)为离散型随机变量．

1．定义

设(X，Y)的所有可能的取值为(x_i，y_j)，则

P｛X=x_i，Y=y_j｝=p_ij i，j=1，2，…

称为(X，Y)的联合分布律．

2．性质

(1)p_ij≥0；

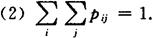
(X，Y)的联合分布函数为

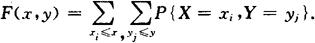
连续型随机变量的联合概率密度函数

若随机变量(X，Y)在某个平面区域(有限或无限)内取所有的值或最多只有有限个点不取，则称(X，Y)为连续型随机变量．

1．定义

设F(x，y)为联合分布函数，f(x，y)≥0，若有

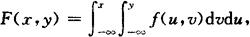
则称f(x，y)为(X，Y)的联合密度函数．

2．性质

(1)f(x，y)≥0；

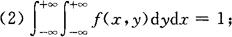
(3)F(x，y)是x，y的连续函数；