二维随机变量的函数的分布
和的分布
已知X,Y的分布,Z=X+Y,求Z的分布.
1.离散型随机变量
已知(X,Y)的联合分布律,或X,Y的边缘分布律.Z=X+Y,Z为离散型随机变量,求Z的分布律.
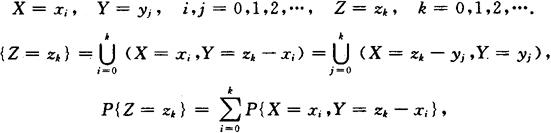
或
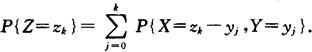
若X,Y相互独立,则有
或
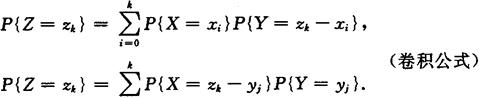
2.泊松分布和的分布,二项分布和的分布
(1)若X~P(λ1),Y~P(λ2),相互独立,则X+Y~P(λ1+λ2).
(2)若Xi~P(λi),i=1,2,…,n,Xi之间相互独立,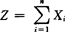 ,则Z~ P(λ),其中
,则Z~ P(λ),其中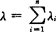 .
.
(3)若X~B(n1,p),Y~B(n2,p)相互独立,则X+Y~B(n1+n2,p).
3.连续型随机变量
若X,Y相互独立,密度函数分别为fX(x),fY(y),Z=X+Y,则有
或
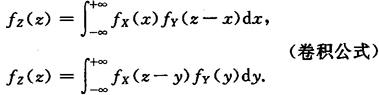
注意:具体计算时,积分限要由密度函数值的非零域来确定.
线性和的分布 若X,Y相互独立,密度函数分别为fX(x),fY(y),Z=aX+bY(ab≠0),则有
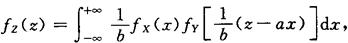
或
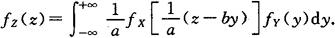
注意:具体计算时,积分限要由密度函数值的非0域来确定.
一般变换定理 设二维随机变量(X,Y)的联合密度函数为f(X,Y)(x,y),并有函数U=u(X,Y),V=v(x,y).如果函数u=u(x,y),v=v(x,y)有惟一的单值反函数x=x(u,v),y=y(u,v),且有连续的一阶偏导数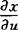 ,
,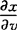 ,
,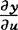 ,
,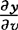 ,则二维随机变量(U,V)的联合密度函数为
,则二维随机变量(U,V)的联合密度函数为
f(U,V)(u,v)=f(X,Y)[x(u,v),y(u,v)]|J|,
其中J为雅可比行列式,即
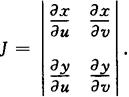
关于U,V的边缘密度函数为
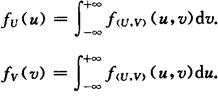
一般函数Z=g(X,Y)的分布
以连续型随机变量为例.设(X,Y)的联合密度函数为f(x,y),Z=g(X,Y),则Z的分布函数为
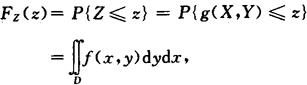
其中D为g(x,y)≤z所表示的平面域.
Z的概率密度函数为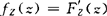 .
.
最大值,最小值的分布
(1)设X1,X2,…,Xn为相互独立的n个随机变量,分布函数分别为FX1(x1),FX2(x2),…,FXn(xn),记
M=maX(X1,X2,…,Xn),
N=min(X1,X2,…,Xn).
M,N的分布函数分别为
FM(z)=FX1(z)FX2(z)…FXnn(z),
FN(z)=1-[1-FX1(z)][1-FX2(z)]…[1-FXn(z)].
若X1,X2,…,Xn同分布,分布函数为F(x),密度函数为f(x),则有分布函数
FM(z)=[F(z)]n,
FN(z)=1-[1-F(z)]n.
M,N的密度函数为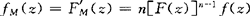 ,
,
fN(z)=n[1-F(z)]n-1f(z).
(2)指数分布的最小值的分布
①设X~E(λ1),Y~E(λ2)相互独立,Z=min(X,Y),则Z~E(λ1+λ2).
②设Xi~E(λi)(i=1,2,…,n),Xi之间相互独立,Z=min{X1,X2,…,Xn},则Z~E(λ),其中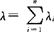 .
.
- 箇失蜜是什么意思
- 箇样是什么意思
- 箇般是什么意思
- 箇诈是什么意思
- 箇谄是什么意思
- 箇里是什么意思
- 箈是什么意思
- 箉是什么意思
- 箊是什么意思
- 箋是什么意思
- 箋子是什么意思
- 箋布是什么意思
- 箋帖是什么意思
- 箋紙是什么意思
- 箋香是什么意思
- 箋麻是什么意思
- 箌是什么意思
- 箌
.jpg) 是什么意思
是什么意思 - 箌
.jpg) 是什么意思
是什么意思 - 箌剥是什么意思
- 箌噘是什么意思
- 箍是什么意思
- 箍上箍头布是什么意思
- 箍住是什么意思
- 箍倒是什么意思
- 箍倚是什么意思
- 箍儿是什么意思
- 箍兜是什么意思
- 箍刀是什么意思
- 箍刀鳞是什么意思
- 箍匠是什么意思
- 箍嘴是什么意思
- 箍围是什么意思
- 箍围疗法是什么意思
- 箍围药是什么意思
- 箍圆是什么意思
- 箍头布是什么意思
- 箍头揽颈是什么意思
- 箍头柴是什么意思
- 箍头管脚是什么意思
- 箍夹是什么意思
- 箍子是什么意思
- 箍屎哕是什么意思
- 箍巴是什么意思
- 箍扎是什么意思
- 箍扣是什么意思
- 箍拐是什么意思
- 箍拐上看脉,事从根上起是什么意思
- 箍拐子子是什么意思
- 箍拢是什么意思
- 箍指病是什么意思
- 箍搂是什么意思
- 箍断效应是什么意思
- 箍桶是什么意思
- 箍桶个是什么意思
- 箍桶刀是什么意思
- 箍桶匠是什么意思
- 箍桶匠工具是什么意思
- 箍桶匠歌是什么意思
- 箍桶匠的本领——成人方圆是什么意思