Chebyshev中心

---

设E是赋范线性空间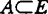，是有界子集，定义：

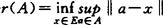
则称r(A)为A的Chebyshev半径，而A的Chebyshe中心就是。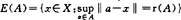

提出这一问题是很自然的。例如，由于试验误差，当我们不能确切地知道函数时，可以把它理解为一个集合，然后用单个的最优元素代表这个集合。另外，Chebyshev中心在最优回复理论的研究中也有重要意义。

Chebyshev中心这一概念首先是Garkavi在1962年提出并研究的，并在1964年给出下面的结果：

定理G Banach空间E中每一有界集A至少有一Chebyshev中心y₀∈COA，当且仅当E是完备内积空间或E的维数2。

下面结果最早是由Kadets和Zamyatin在1968年对S=［a，b］给出的，一般情形是由Franchetti和Cheney给出的。

定理K－Z：B(S)(C(S)中任一有界集恒有非空的Chebyshev中心，其中S是任一拓扑空间，B(S)(C(S))是全体实有界(连续)函数所组成，并赋于一致范数。

对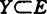，A的相对或限制(Chebyshev中心)，是

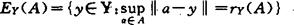
其中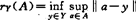，，为A的相对或限制Chebyshev半径。这一问题自60年代就有许多研究。

关于唯一性，1980年Amir和Ziegler定义了E关于子空间Y的严格凸性和各向一致凸性。

定理A－Z 设Y是E的子空间，则：(1)对任何紧子集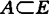，E_Y(A) 至多只有一个元当且仅当E关于Y是严格凸；(2)对任何有界集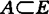，E_Y(A) 至多只有一个元当且仅当E关于Y是各向一致凸的。

关于相对Chebyshev中心的特征，当A是局部紧时，由于可转化成C(A、E)中的单元逼近，故可以毫无困难地得Kolmogorov型特征定理。但对一般的有界集A，要给出其Kolmogorov型特征定理并非易事。

1982年，Freilich和McLaughlin在Y是凸集时给出下列的Kolmogorov型特征。

定理F－M y₀∈E_y(A)当且仅当对任何y∈Y存在L∈extK满足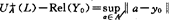且ReL(y－y₀)≤0，其中的闭单位球B^*。

在K上赋以σ(K、G)拓扑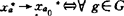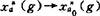：，，且K满足：(1)K是σ(K、G)紧。(2)任何a∈A，y∈Y，有。

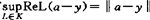而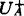(L)定义为：

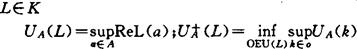
其中U(L)为在K上的开例域全体。

但定理F－M中的必要性未必成立，我们在1987年举例说明不真，并刻划了非线性情形下的相对Chebyshev中心的特征。

定理X－L 设Y是E中一子集，则下述论断等价：(1)对任何有界集F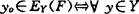，，存在L∈Y，使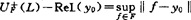且ReL(y－y₀)≤0；(2)Y是同时太阳集。即对任何有界集F，若y₀∈E_Y(F)，则y₀∈E_Y(F_a)，其中F_a=y₀+a(F－y₀)，a≥0。

关于Er(A)的非空性，即相对Chebyshev中心的存在性。

若有某种紧性，例如局部有界紧或局部有界弱紧，且Y是闭或弱闭，则对任何有界集A，EY(A)非空。

但是当Y没有任何紧性，则其研究相当困难。1991年，D．V．Pai和P．T．Nowrojij在E中的子空间Y引进R₁性质，这是单元逼近中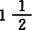一球性质的推广，并证明了下面的存在性定理。

定理P－N 设E是Banach空间，Y是E的子空间，若Y关于E中所有的有界集(紧集)有R₁性质，则对任何有界集(紧集)A，E_Y(A)≠Φ。

目前有众多的文献在研究EY(A)的连续性与强唯一性，对E中任何两个有界集A、B，其Hausdorff距离定义为：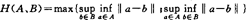

1982年，P．Szeptycki和F．S．Var VLeck证明了下述定理。

定理S－V 若E是Hilbert空间，则对任何两个紧子集A、B有

‖ E(A)－E(B)‖²≤［r(A)+r(B)+H(A，B)］H(A，b)(*)

并提出下述两个问题

问题S－V－I：若A、B没有紧性(*)式是否成立?

问题S－V－I：当E是一致凸空间时，‖E(A)－E(B)‖是否有类似于(*)式的估计?

1988年，我们给问题S－V－I一个肯定回答；

定理L：设E是Hilbert空间，Y是E中凸集，则对任何有界集A，B有

‖E_r(A)－E_r(B)‖²≤［rY(A)+rY(B)+H(A，B)］H(A，B)

问题S－V－Ⅱ，在1989年由王嘉平与俞鑫泰解决。

在当前及今后的研究中，相对Chebyshev中心的定量分析，如相对Chebyshev中的实现，相对Chebyshev半径的计算等，将成为热点和趋势。

。【参考文献】：

1 Garkavi A L, The Chebyshev centers and the convex hull of a set,Uspehi Mat Nauk,1964,19:139-145

2 Amir D , Ziegler Z. Relative Chebyshev Centers in Normed Linear Space I,J Approx Theory, 1980,29:235-252

3 Franchetti C , Cheney E W. Simultaneous approximation and restricted Chebyshev centers in fanction spaqes, in " Approximation Theory andd Applications", ed. by Z Ziegler,Academic Press, New. York, 1981, 65～88

4 Freilich J H , Mclaughlin H W. Approximation of bounded sets,JApprox Theory,1982,34:145～158

5 Franchetti C , Cheney E W.The embedding of Proximinal sets J Approx Theory, 1986,48:213～225

6 徐士英，李冲，等．最佳同时逼近的特征．数学学报，1987，30(4)∶528～535

7 Szeptycki P , Van Vleck F S: Centers and nearest points of sets,Proc A,M,S,85 1987,8S:27～31

8 Li Chong. On a problem on Chebyshev centers, Advance in Math,1988,17(2) ,216～217

9 Wang J P, Yu X T. Chebshev centers, Chebyshev centers and the Hausdorff metric,Manuscripta Math, 1989,63:115 ～128

(杭州商学院李冲副教授撰；徐士英审)