非线性回归预测法

---

亦称“曲线式最小平方法”，即运用最小二乘法，求出倾向变动曲线，作为外推依据来进行预测。

倾向变动曲线方程一般为：

Y=a+bx+cx²

通常用下式求解上式中的a、b、c数值。

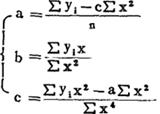
有时非线性回归分析可用变量置换办法，把非线性问题转化成线性问题来求解。

例：盛钢水的钢包，在使用过程中，由于钢水的侵蚀，容积不断增大，其使用次数X与钢包容积增大量Y之间的数据如表所示。现要求找出次数X与容积增大量Y之间的关系，并建立预测模型。

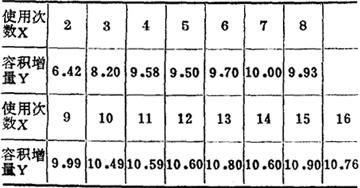
从上表可看到，最初容积增大较快，以后逐渐减慢。当然钢包容积不会无限增大，即曲线必有一条平行于X轴的渐近线，选双曲线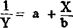：为拟合曲线。

并令

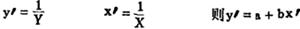
因此可用线性回归类方法求出a和b的值(详见“线性回归分析预测法”)。

计算结果为：a=0．0823b=0．1315

回归方程为：y′=0．0823+0．1315x′

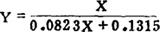
标准离差

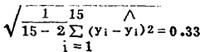
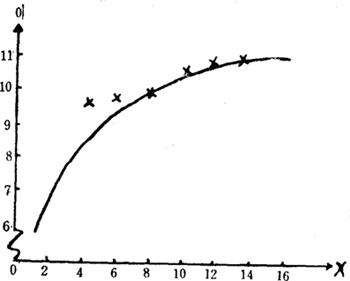
按表作散布图如下：