集中量数

---

亦称平均数(averages)。

描述某数据分布集中趋势的数值。集中趋势是数据分布的一项重要特征，反映数据分布集中趋势特征值的平均数，是数据资料的代表性数值或典型水平。计算平均数，要求所研究的事物应属于同质的总体。常用的平均数有：
❶ 算术平均数(arithmetic mean)，是应用最广泛的平均数，它是数据资料中各个数值的总和除以数值个数所得之商。通常简称为平均数，只有在与其他种平均数相区别时，才称之为算术平均数。如数据资料已归类分组编成频数分布表，设X₁，X₂，…X_n为各组的组中值，f₁，f₂，…f_n为各组的频数，这时按下列公式计算加权算术平均数(#)：==。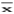

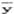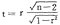公式中，各组的频数f，为加权算术平均数的权数；
❷ 几何平均数(geometric mean)，是N个数值连乘积的N次方根，主要用于计算经济指标的平均发展速度和某种比率的平均数；
❸ 调和平均数(harmonic mean)，各个数值的倒数的算术平均数的倒数，也称倒数平均数，主要用于计算按倒数表示的平均价格(如平均每元买几斤桃子)与平均速度；
❹ 中位数(median)，数据按大小顺序排列，正处于中间地位的数值，又称"中数"。有一半的数值小于中位数，另一半的数值大于中位数，因而它可以表示数据资料的集中趋势；
❺ 众数(mode)，是数据资料中出现次数最多的数值。

它是最常见的数值，也能反映数据资料的集中趋势。

根据数学上的特征，前三种叫做计算的平均数(computed averages)，后两种叫做位置平均数(Position averages)。