递归定义

---

给命题公式下定义的一种。

例如：

(1)命题变元是公式；

(2)如果A和B是公式，那么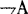，，(A∧B)，(A∨B)，(A→B)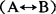，也是公式。

(3)所以，根据定义1与定义2而组成的式子也都是公式。

上面依次做出的规定就是递归定义。

递归定义，主要是用来规定函数的。

是以二重方式组合起来的隐含定义(见《隐定义》)。如果给出数学函数f(x)的一个值f(1)，并且如果在f(x)和f(x+1)之间存在著这样的关系，那么根据f(x)的值可以确定f(x+1)的值，我们便说这是f(x)的递归定义。

要做出一个递归定义，首先应给被定义的函数f(x)规定出适合于数列首项的值，然后再给函数f(x)规定出适合于任意项的后继项的值。

递归定义在算术中起著特殊的作用。

例如，根据自然数和利用顺序关系(设自然数a之后的=个数是a’)，我们就可以给加法做出如下精确的定义：

a+1=a’

a+(n+1)=(a+n)’

递归定义只适用于与自然数的性质直接有关的对象，超出了这个范围，递归定义就不能成立。