(1)达西实验定律
法国水力学家达西在1856年研究流经装填有均匀砂粒(砂滤)的垂直管内的水流时,得出了著名的达西定律
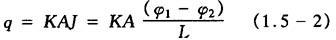
式中 q——水的流量;
K——固有渗透系数,其量纲为[L/T];
A——管的截面积;
J——水力梯度,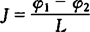 ;
;
φ——测压管水头,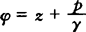 ,其中z为从水平基准面算起位置高度,户/γ为压力水头;
,其中z为从水平基准面算起位置高度,户/γ为压力水头;
L——含砂粒层的管道长度。
适用于其它液体有压渗流的流动,常将式(1.5-2)改为

式中 μ——液体的粘度;
k——渗透率,其量纲为[L2],若在1个大气压/cm(0.1MPa/cm)的压力梯度下,将粘度为1cP的液体,经每1cm2的截面积渗透过1cm3/s的流量时的k值称为1达西。
而渗透率k与渗透系数K的关系

式中 v——液体的运动粘度;
g——重力加速度。
多孔物质的渗透率与物质的空隙率n,液体的物性和流动的雷诺数Re=vd/v有关,Re中的d为组成多孔物质的颗粒直径。k值可按欧根(Ergun)方程来估算,即
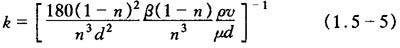
当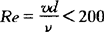 时的层流
时的层流
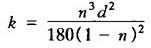
当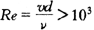 为湍流时
为湍流时
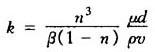
式中 d——多孔物质的颗粒直径;
ρ——液体密度;
β——无量纲参数,对于光滑颗粒取β=1.8,对粗糙颗粒取β=4。
k值也可按表1.5-2查得。
(2)高雷诺数(Re>10)的渗流计算
当雷诺数Re>10以上时,线性的达西定律则有所偏离。尤其是Re>100时,达西定律已不适用。很多学者作了大量的实验研究,则用“渗流的二项式定律”代替达西定律。
欧根1952年提出下式
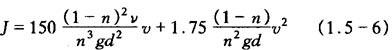
式中 v——液体的运动粘度:
d——多孔物质的颗粒直径;
v——液流平均流速。
奥迈德(Ahmad)1967年提出下式
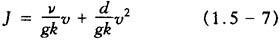
- H003553 日语词汇论是什么意思
- H003554 日语用言用例是什么意思
- H003555 日语基础句型浅说是什么意思
- H003556 日语助词用例是什么意思
- H003557 日语简明教程是什么意思
- H003558 日语词汇学是什么意思
- H003559 日语基础是什么意思
- H003564 日语会话常用词语用例辞典是什么意思
- H003566 日语拟声词拟态词辞典是什么意思
- H003568 实用日汉双解词典是什么意思
- H003570 现代日本语教程是什么意思
- H003572 日语缩略语词典是什么意思
- H003574 日本古典文法是什么意思
- H003575 常用日汉辞典是什么意思
- H003576 大学日语是什么意思
- H003579 现代日语实用语法是什么意思
- H003580 日汉大辞典是什么意思
- H003583 现代日汉汉日词典是什么意思
- H003584 日语同义词辨析是什么意思
- H003585 袖珍中日熟语词典是什么意思
- H003586 日本汉字读音辞典是什么意思
- H003589 日汉小词典是什么意思
- H003590 两天一课日语自学速成课本是什么意思
- H003591 袖珍日汉汉日词典是什么意思
- H003592 研究生日语是什么意思
- H003593 日汉对照基础日本语学习词典是什么意思
- H003594 刘耀武日语语法论文集是什么意思
- H003595 最新日朝辞典是什么意思
- H003597 速查日汉辞典是什么意思
- H003602 日语贸易洽谈是什么意思
- H003603 现代日语基础语法是什么意思
- H003605 日汉反义词词典是什么意思
- H003607 日语听力Ⅰ是什么意思
- H003608 新汉日词典是什么意思
- H101 脱脂剂是什么意思
- H102 系列柔软剂是什么意思
- H2O2的生产与供应是什么意思
- H302顶层手感改善剂是什么意思
- ha是什么意思
- Habeas corpus是什么意思
- habit是什么意思
- habit是什么意思
- habit是什么意思
- habitual是什么意思
- habitual是什么意思
- hab·it是什么意思
- hack是什么意思
- had是什么意思
- Hadamard矩阵猜想是什么意思
- hail1是什么意思
- hail2是什么意思
- hair是什么意思
- hair是什么意思
- hair是什么意思
- hair是什么意思
- haircut是什么意思
- hairy是什么意思
- half是什么意思
- half是什么意思
- half是什么意思