费希尔判别

---

判别分析的一种方法。

费希尔判别利用降维和方差分析的思想建立线性判别函数，对降维后的总体利用距离判别建立判别规则，并以此对样品(被试)作出归属何个总体的判别分析。设有k个p维总体G₁，G₂，…，G_k，样本均值分别为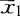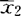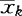，，…，，样本协方差矩阵分别为S₁，S₂，…，S_k。

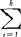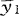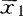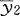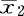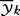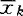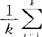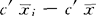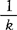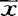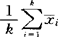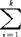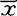考虑样品x=(x₁，x₂，…，x_p)′的p个变量的线性组合y=c′x=c_ix_i，它将p维空间的点变换为直线上的点(降维)，变换后总体G₁，G₂，…，G_k的样本均值分别为=c′，=c′，…，=c′，样本方差分别为c′S₁c，c′S₂c，…，c′S_kC。描述变换后各总体间差异的指标是方差()²=c′Bc，其中=_i，B=(x_i－)(x_i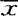－)′。描述变换后各总体内差异的指标是各总体变换后方差的平均值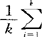c′S_ic=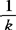c′Wc，其中W=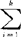S_i。变换后总体间差异与总体内差异的比值Δ(c)=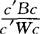称为判别效率函数。费希尔判别是要使判别效率函数Δ(c)达到极大。这样的c(如果有的话)不是唯一的，为确定起见，加上约束条件c′Wc=1，即判别效率函数中的分母等于1。

设λ₁≥λ₂≥…≥λ_s＞0为矩阵W^－1B的非零特征根，e₁，e₂，…，e_s为相应的特征向量(满足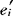We_i=1)。可以证明，当c取为矩阵W^－1B的最大特征根λ₁对应的特征向量e₁(满足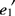We₁=1)时，Δ(c)达到最大值λ₁。称y₁=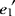x为第一判别函数。若这个线性判别函数还不能很好区分各个总体，可取λ₂对应的特征向量e₂建立第二判别函数y₂=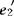x。

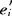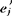若还不够，依此类推，可建立多个判别函数，这样得到的判别函数方差为1，且彼此不相关，即Cov(y_i，y_j)=Cov(x，x)=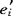We_j=0，(i≠j)。设共有r个判别函数，它们将原来的p维空间的点x=(x₁，…，x_p)变成r维空间的点y=(y₁，…，y_r)。对于总体G_i，变换后(仍记为G_i)的样本均值为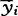=(e₁′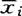，…，e_r′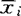)，样品x₀变换为y₀=(y₀₁，…，y_0r)，y₀到总体G_i的距离(注意到y=(y₁，…，y_r)的协方差矩阵为单位矩阵，马氏距离即为欧氏距离)平方为d²(y₀，G_i)=(y₀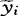－)′(y₀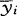－)，i=1，…，k。这样，在变换后的空间中应用距离判别，就得到费希尔判别的规则：若d²(y₀，G_i)=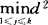(y₀，G_j)，则将x₀判归总体G_i，i=1，…，k。

若各总体的协方差矩阵相等，则判别效率函数中的W取为混合类内协方差矩阵(即把k个样本合并为一个样本来计算协方差矩阵)。对于两个有相同协方差矩阵的正态总体，费希尔判别结果与距离判别结果一致。