线性规划模型

---

由决策变量、约束条件、目标函数构成的描述线性规划问题的数学模型。

其标准形式为：求一组决策变量x₁，x₂，…，x_n的值，满足约束条件：

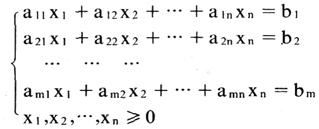
使目标函数

Z=C₁X_i+C₂X₂++C_nX_n→最大

其中：a_ij，b_i，c_i(1=1，2，…，m；j=1，2，…，n)是给定的参数。an为决策变量的约束条件系数，ci为决策变量的目标函数系数，b_i为常数项，始终要求b_i≥0，即满足可行状况。

由实际问题抽象得到的模型不一定是标准形式。

化标准形式的方法有：(1)在约束线性不等式的左端加入(如约束不等式为<)或减去(如约束不等式为>的辅助变量x_n+1，化不等式为等式，辅助变量在目标函数中的系数c_n+1规定为0，使之不影响最优解；(2)如果对某一变量x_j(1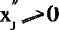，，令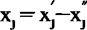，代入约束方程及目标函数中，化全部变量为非负约束，(3)如果某个常数项b_i(1*=－Z的最大值。

用单纯型法求解线性规划问题，必须先将数学模型由非标准形式化为标准形式。