线性约束回归

---

经济理论或实践有时要求回归模型的系数要满足某些线性等式约束的条件。

例如：柯布－道格拉斯生产函数#

这里Y为产量，K为资本投入量，L为劳动投入量，u为随机扰动项，e为自然对数的底。采用对数形式表示为

lnY_i=lnα+β₁lnK_i+β₂lnL_i+u_i

如果已知在所研究的时段内规模报酬是不变的，那么回归方程就要遵守约束

β₁+β₂=1

对于上面这种简单的约束回归模型，可以直接把约束条件代入方程，化为无约束的普通回归方程来求解；但是对于较为复杂的约束回归模型，就要找出一般求解公式。

一般说，对于线性回归模型

Y=Xβ+u

若约束条件为

Rβ=r

此处R为常数矩阵(维数与β相对应)，r为常向量，那么根据最小二乘原理，利用拉格朗日求条件极值的方法，得到

β^*=β+(X′X)^－1R′[R(X′X)^－1R′]^－1

(r－R β)

这就是有约束条件的最小二乘估计式，其中β表示无约束条件下的最小二乘估计式。

对于约束条件的假设检验，可采用F－检验。构造F统计量

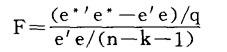
其中e^*为有约束条件下作最小二乘估计所得的残差，e为无约束条件下作最小二乘估计所得的残差，q为约束条件的个数。可以证明

F～Fq，(_n－k－1)