线性模型

---

确立因变量对于自变量的依赖关系是一类广泛存在而且有重要意义的问题。

在很多情况下，这种关系不能从理论分析中得到，而要利用数据去拟合。在这样做的时候首先要建立模型，模型中含有若干未知参数。

然后利用数据估计未知参数的值，并检验模型的合理性。模型中的未知参数业经求出并通过检验，就可利用模型进行预测。

一类很重要的模型是具有线性结构的模型，称作“线性模型”。

把因变量记作y。

设自变量有k个，x₁…，x_k，f_j(x_1m，…，x_k)为已知函数，j=i，p。设y与x₁，…x_k之间具有关系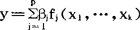：其中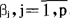，是未知参数。

当自变量x1，…xk取得观察值时，f_j(x₁，…，x_k)，j=1，p，便成为已知的数，问题是要利用观察数据求出未知数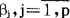。设一共进行了几次观察，在第i次观察中，自变量的值为x₁₁，…，x’_ki，因变量的值为Y_i。在观察中总会有无法控制的随机误差，如果所建立的模型正确，则观察值之间有下面的关系：

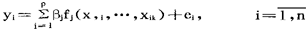(1)

其中e_i是第i次观察的误差，是随机变量。既然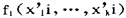是由观察值确定的已知数，为简单起见，记作x_ij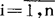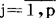，，，则(1)成为

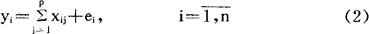
对于观测误差常根据问题的实际情形提出一些假设，常见的假设有以下两种：

(1)设e₁…，e_n独立同分布，且Ee_i=0，var(e_i)=σ²，0＜σ²＜∞，σ²未知，

(2)e₁…，e_n满足(1)，且它们共同的分布是均值为0的正态分布。

记

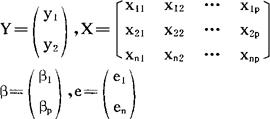
则(2)可简化为

Y=X_β+e

(3)(或(2)或(1))称作线性模型，这里的线性是针对未知参数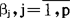而言的，未知参数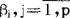以其线性函数的形式出在在模型中。σ²也是模型的一个未知参数。求解线性模型的任务有两方面，一是估计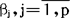及σ²；二是关于参数β_j的假设检验。