系统频率特性线图的绘制

---

2．7．1 系统的开环幅相图

例1．9－8 已知系统的开环传递函数为

当给出一系列ω值时，由以上两式可算出一系列相应的开环幅值和开环相角，据此可画出该系统开环幅相图，如图1．9－23统示。

显然，用这种方法绘制准确开环幅相曲线是很麻烦的，因此在一般情况下可根据开环幅相频率特性曲线的特点，来绘制概略开环幅相图。

2．7．2 系统的开环对数坐标图

系统的开环对数频率特性曲线绘制步骤和方法如下：

❶ 将传递函数写成典型环节的乘积形式。

❷ 选定坐标轴比例尺。

❸ 计算开环增益(开环放大倍数)k的分贝值和各典型环节的交接频率。

❹ 绘制频率从0至最小交接频率的渐近线。该渐近线是一条在频率ω=1处的幅值为201gk，斜率为n×(±20)dB／(+倍频程)的直线(系统开环传递函数中含有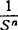取－，含有S”取+)。

❺ 在各典型环节交接频率处依次改变渐近线斜率，遇惯性环节斜率要在原基础上再改变－20dB／+倍频程，遇一阶微分环节要在原基础上再改变+20dB／+倍频程，遇振荡环节要在原基础上再改变－40dB／+倍频程。

❻ 振荡环节阻尼比较小时，必须对渐近特性曲线进行修正。

❼ 系统开环相频特性曲线由各典型环节相频特性叠加而成。

例1．9－9 已知系统开环传递函数为

在频率ω=1处，找到纵坐标等于201gK=20dB的点，过该点作斜率为－20dB／(+倍频程)的直线。再在各交接频率处依次改变斜率画出开环对数幅频特性渐近线。在ω₁=0．5处，曲线斜率由－20dB／(+倍频程)变为－40dB／(+倍频程)；在ω₂=1处曲线斜率由－40dB／(+倍频程)变为一20dB／(+倍频程)；在ω₃=20处，曲线斜率由－20dB／(十倍频程)变为－60dB／(十倍频程)。由于本例振荡环节阻尼比ζ=0．35，阻尼比较小，因此应在振荡环节交接频率处及其附近对渐近线进行修正，系统对数幅频特性如图中L(ω)所示，

该系统中比例环节的相频特性φ₁(ω)=0°；积分环节相频特性φ₂(ω)=－90°；惯性环节的相频特性φ₃(ω)=－arctgωT=－arctg2ω；一阶微分环节的相频特性φ₄(ω)=arctgωT=arctgω；振荡环节的相频特性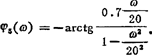，根据上述各式分别作出各典型环节的相频特性曲线φ₁～φ₅，然后将各典型环节在同一频率下的相角作代数加法，画出系统的开环相频特性曲线如图中φ(ω)所示。

2．7．3 系统的闭环频率特性

图1．9－25所示是系统闭环幅频特性曲线，图中，M_p为闭环系统的谐振峰值；ω_p为闭环系统的谐振频率；ω_b为闭环系统的带宽频率，是闭环幅频特性值下降到频率为零时的闭环幅频特性值的0．707倍时的频率，即M(ω_b)=0．707M(o)，分析研究系统时，有时需要使用上述闭环频域指标，闭环频率特性曲线可利用如等M圆图、等N圆图、尼柯尔斯图等标准图线绘制，如果应用计算机的标准程序绘制系统的各种频率特性曲线，则更为方便，图1．9－26所示，为用FORTRAN语言计算开环和闭环频率特性的流程图。