简单随机抽样平均误差

---

在简单随机抽样调查的组织形式下，抽样平均数或抽样成数的均方差，它们的计算公式随抽样的方法不同而异。

在重复抽样的条件下，数理统计证明，抽样平均误差，等于全及总体平均数均方差(σ)除以抽样单位数(n)的平方根。如下式：

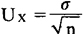
对于不重复抽样，抽样平均误差公式为：

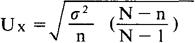
式中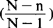叫做修正系数。当总体单位数较多时，系数中的分母N－1可用N代替，这时上式可简化为：

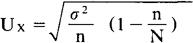
在掌握抽样平均数平均误差计算方法的基础上，探求抽样成数平均误差的公式是比较简便的。

理论证明，全及成数的方差为P(1－P)，将此代替上式中的σ²，就可得到以下两个计算抽样成数平均误差的公式：

重复抽样时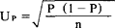

不重复抽样时

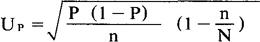
由于(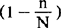)这个数值永远小于1，所以在同样的情况下，不重复抽样的平均误差，永远小于重复抽样的平均误差。

如果N很大，n相对很小时，则(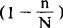)接近于1，对于平均误差的作用不大。因此实际工作中按不重复抽样方法抽样时，也往往采用重复抽样的公式计算抽样平均误差。