1.形如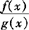 >0型
>0型
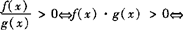
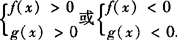 .
.
2.形如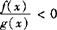 型
型
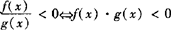
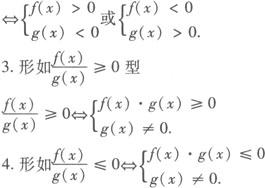
例1 解下列不等式
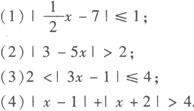
分析 (1)、(2)、(3)中可把1/2x—7,3—5x,3x—1看作一个整体.(4)由x—1=0,x+2=0可得x=1,x=—2,1和—2把数轴分成三段,每一段上决定了x—1和x+2的正负,由绝对值的定义去掉绝对值号即可.
解 (1)|1/2x—7|≤1等价于—1≤1/2x—7≤1,
解得12≤x≤16.
..原不等式的解集为{x}12≤x≤16}.
(2)原不等式等价于3—5x<—2或3—5x>2,
解得x>1或x<1/5.
∴原不等式的解集为{x|x<1/5或x>1}.
(3)从形式上看与(1)、(2)有所不同,为使运算简便,令u=3x—1,则2<|u|≤4,此式等价于|u|≤4且|u|>2即—4≤u≤4且u<—2或u>2,解得—1≤x≤5/3且x<—1/3或x>1,如下图所示:
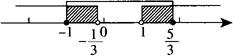
∴原不等式解集为
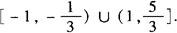
(4)原不等式等价于
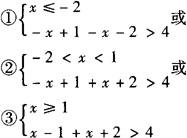
解❶ 得x<—5/2;解❷ 得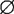 ;解❸ 得x>3/2.
;解❸ 得x>3/2.
∴原不等式解集为{x|x<—5/2或x>3/2}.
例2 解下列不等式
(1)4x2—4x>15;
(2)4x≤1+4x2;
(3)—x2+x—1>0;
(4)0
解 对于(1)、(2)、(3)可直接利用二次不等式,二次函数关系求解.(4)可转化为不等式组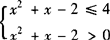 求解.
求解.
(1)原不等式可化为4x2—4x—15>0
∵a=4>0,又方程4x2—4x—15=0的解是:
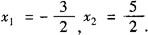
∴原不等式的解集是
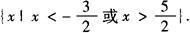
(2)原不等式可化为4x2—4x+1≥0.
∵a=4>0,又方程有两等根x1=x2=1/2,
∴原不等式的解集为R.
(3)原不等式可化为x2—x+1<0.
∵a=1>0又△=1—4=—3<0,
∴原不等式的解集是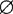 .
.
(4)原不等式可能转化为不等式组.

解❶ 得x>1或x<—2
解❷ 得—3≤x≤2.
∴原不等式的解集为
{x|—3≤x<—2或1 例3 解关于x的不等式|3x—2|<2m1(m∈R). 解 这里没有2m—1>0的条件,必须分类讨论: (1)当2m—1≤0即m≤1/2时,原不等式恒不成立, ∴ (2)当2m—1>0即m>1/2时,原不等式可化为—(2m—1)<3x—2<2m—1,解得 综上所述,当m≤1/2时,原不等式的解集为 当m>1/2时,原不等式的解集为: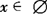 .
.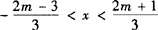 .
.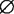 ,
,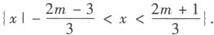
- 妙灵丸(1)是什么意思
- 妙灵丸(2)(妙灵丹)是什么意思
- 妙灵丹是什么意思
- 妙灵丹是什么意思
- 妙灵丹是什么意思
- 妙灵丹是什么意思
- 妙灵丹是什么意思
- 妙灵丹是什么意思
- 妙灵散是什么意思
- 妙灵散是什么意思
- 妙灵散是什么意思
- 妙灵散是什么意思
- 妙玉是什么意思
- 妙玉是什么意思
- 妙玉是什么意思
- 妙玉是什么意思
- 妙用是什么意思
- 妙用膏是什么意思
- 妙真法师是什么意思
- 妙算姜维不等闲是什么意思
- 妙绝时人是什么意思
- 妙胜散是什么意思
- 妙胤是什么意思
- 妙能映合本题是什么意思
- 妙色王是什么意思
- 妙草散是什么意思
- 妙药奇方是什么意思
- 妙觉寺舍利塔是什么意思
- 妙计杀蛇精是什么意思
- 妙语天下是什么意思
- 妙语惊人是什么意思
- 妙语解颐是什么意思
- 妙语解颐是什么意思
- 妙语解颐是什么意思
- 妙语连珠是什么意思
- 妙贴散是什么意思
- 妙贴散是什么意思
- 妙贴散是什么意思
- 妙趣是什么意思
- 妙趣横生是什么意思
- 妙趣横生是什么意思
- 妙趣横生是什么意思
- 妙道是什么意思
- 妙顶是什么意思
- 妙香丸是什么意思
- 妙香丸是什么意思
- 妙香丸是什么意思
- 妙香丸是什么意思
- 妙香丸是什么意思
- 妙香丸是什么意思
- 妙香丸是什么意思
- 妙香丸是什么意思
- 妙香丸是什么意思
- 妙香室丛话是什么意思
- 妙香室丛话是什么意思
- 妙香山是什么意思
- 妙香散是什么意思
- 妙香散是什么意思
- 妙香散是什么意思
- 妙香散是什么意思