等轴双曲线

---

实轴和虚轴相等的双曲线叫做等轴双曲线．

例1 设双曲线与椭圆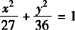有共同焦点，且与此椭圆一个交点的纵坐标为4，求这个双曲线的方程．

策略 先求出椭圆的焦点坐标，即双曲线的焦点坐标，再定双曲线标准方程的形式，利用条件求待定系数a，b．

解 由已知得双曲线两焦点分别为F₁(0，—3)，F₂(0，3)．

设双曲线的方程为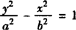(a>0，b>0)，

∵双曲线与椭圆有一交点纵坐标为4，

∴它们交点为．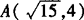

∵||AF₁|—|AF₂||=2a，

∴将A、F₁、F₂的坐标代入得a=2，

又∵c=3，

∴b²=c²—a²=5．

故所求双曲线的方程为．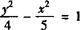

例2 已知双曲线关于两坐标轴对称，且与圆x²+y²=10相交于点P(3，—1)，若此圆过点P的切线与双曲线的一条渐近线平行，求此双曲线的方程．

解 切点为P(3，—1)的圆x²+y²=10的切线的方程是3x—y=10．

∵双曲线的一条渐近线与此直线平行，且双曲线关于两坐标轴对称，

∴两渐近线的方程为3x±y=0．

设所求双曲线的方程为9x²—y²=λ．

∵点P(3，—1)在所求的双曲线上，

∴λ=9×3²—(—1)²=80．

∴所求双曲线的方程为9x²—y²=80，即．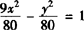

例3 已知A、B、C是我方三个炮兵阵地，A在B的正东，相距6km，C在B的北偏西30°，相距4km，P为敌炮阵地，某时刻A处发现敌炮阵地的某种信号，由于B、C两地比A距P地远，因此4s后，B、C才同时发现这一信号(该信号的传播速度为1km/s)，A若炮击P地，求炮击的方位角．

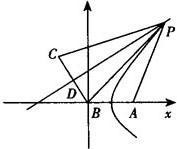
解 如图所示，以BA所在直线为x轴，过点B垂直于直线BA的直线为y轴建立直角坐标系，单位长度为千米，则点B、A、C的坐标分别为(0，0)，(6，0)，(—2，)．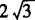

∵|PB|=|PC|，

∴点P必在线段BC的垂直平分线上．

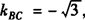∵，BC中点，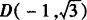

∴直线PD的方程为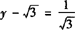(x+1)． ❶ 

又∵|PB|—|PA|=4，

∴点P必在以点A、B为焦点的双曲线的右支上，设P点坐标为(x，y)，双曲线方程为：

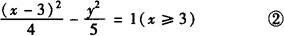
联立式❶ 、❷ 解方程组

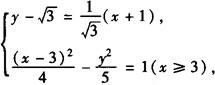
∴炮击的方位角为东偏北60°．

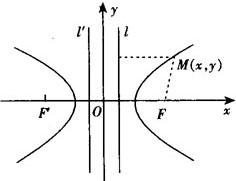
例4 双曲线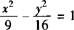右支上有一点P，P到左焦点的距离为11，求点P到右准线的距离．

策略 将双曲线的第一定义与第二定义综合运用

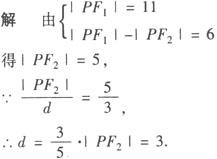
故点P到右准线的距离为3．