直线与平面垂直的判定定理

---

定理1 如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面，用符号表示为

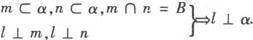
定理2 如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于同一个平面，用符号表示为a∥b，．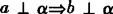

例 在正方体A₁B₁C₁D₁—ABCD中，E，F分别是棱AB，BC的中点，O是底面ABCD的中心，求证：EF⊥平面BB₁O．

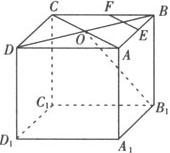
策略 利用两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面，本题可选证AC⊥平面BB₁O，再证EF∥AC即可．

证明 如图，连结AC，BD，则O为AC，BD的交点．

∵四边形ABCD为正方形，∴AC⊥BO．

又∵BB₁⊥平面ABCD，AC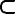平面ABCD，∴AC⊥BB₁．

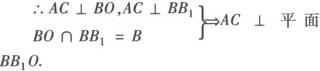
又∵EF是△ABC的中位线，∴EF∥AC，

∴EF⊥平面BB₁O．

点评 由EF⊥平面．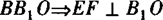

本题也可连AB₁，CB₁，由CB₁=AB₁，CO=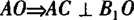，请读者按此思路自己完成证明．