用导数研究函数的极值

---

利用导数求函数极值的方法和步骤如下：

1．求导数f′(x)；2．求方程f′(x)=0的根；3．检查f′(x)在方程根左、右的值的符号，如果左正右负，那么f(x)在这个根处取得极大值，如果左负右正，那么f(x)在这个根处取得极小值，如果左右同号，那么f(x)在这个根处无极值．

例1 求y=4x³—x²—2x的极值点和相应的极值．

解 ∵y′=12x²—2x—2，∴在(—∞，+∞)内任一点处都可导，所以它的极值点就是其导数等于0的点，但要注意导数为0的点并非都是极值点，必须考察导数等于0的点的左右导数的符号和函数的单调性．

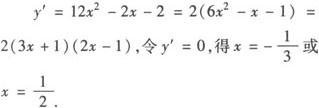
∴当x变化时，y，y′的变化情况如下表：

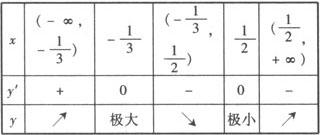
例2 已知函数f(x)=x³+ax²+bx+c，当x=—1时取得极大值7，如x=3时取得极小值，求极小值及这时a，b，c的值．

解 依题意x=—1与x=3是方程f′(x)=0的两根，于是先求出f′(x)，再由f′(—1)=0，f′(3)=0，求出a，b，c．

∵f(x)=x³+ax²+bx+c，

∴f′(x)=3x²+2ax+b

∵x=—1时，函数取得极大值，x=3时取得极小值，

∴—1，3是方程f(x)=0的两根．

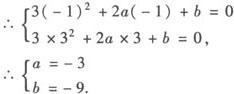
∴f(x)=x³—3x²—9x+c．

又x=—1时，y_极大=7，∴(—1)³—3(—1)²—9(—1)+c=7，∴c=2．

y_极小=f(3)=3³—3×3²—9×3+2=—25．

故a=—3，b=—9，c=2，y_极小=—25．