用代入消元法解二元一次方程组的步骤

---

1．求表达式：选取系数比较简单的方程进行变形，用含一个未知数的代数式表示另一个未知数．

2．代入消元：将求得的表达式代入另一个方程，得到一个一元一次方程，并求解．

3．回代求解：将求出的未知数的值代入变形后的表达式中，求出另一个未知数的值，从而得到方程组的解．

例1 用代入法解方程组

解 由❶ 得y=7－x．❸ …求表达式

把❸ 代入❷ ，得2x－(7－x)=2．…代入消元

2x－7+x=2，3x=9，x=3．

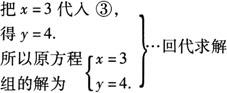
[解析] 解方程组最后必须总结原方程组的解是什么．

例2 解方程组

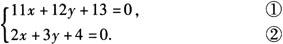
解 ❶ 式变形为4(2x+3y+4)+3x－3=0．❸ 

把❷ 代入❸ 得3x－3=0．

x=1．

把x=1代入❷ 

得2+3y+4=0．

y=－2．

所以原方程组的解为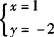

[解析] 比较复杂的题目可以选择整体代入法．