模糊数学中的基础概念。
指给定了论域U上的一个模糊子集A,对于任意u∈U,都指定一个称之为u对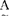 的隶属程度的数UA(u)∈[0,1]。映射μA:U→[0,1]叫作A的隶属函数。模糊子集完全由其隶属函数所刻划,当μ
的隶属程度的数UA(u)∈[0,1]。映射μA:U→[0,1]叫作A的隶属函数。模糊子集完全由其隶属函数所刻划,当μ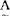 的值域={0,1}时,A便蜕化成一个普通子集,μ
的值域={0,1}时,A便蜕化成一个普通子集,μ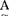 X为其特征函数。于是,设∮(U)和
X为其特征函数。于是,设∮(U)和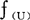 分别为U上的全体普通子集和全体模糊子集所构成的类,则有:
分别为U上的全体普通子集和全体模糊子集所构成的类,则有: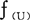
 ∮(u)且当
∮(u)且当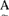 ∈
∈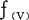 -∮(U)时,
-∮(U)时,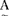 叫作真模糊子集。
叫作真模糊子集。
当论域U有限时,设U={a1,a2,……an},则U上的一个模糊子集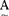 表为:
表为: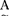 =μ
=μ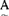 (a1)/a1+μA(a2)/a2+……+μA(an)/an当论域U是无限时,使用记号
(a1)/a1+μA(a2)/a2+……+μA(an)/an当论域U是无限时,使用记号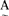 =∫(μA(u)/u)来表示U上的一个模糊子集A,当然,表示的方法还有许多,并且各有优点。模糊子集的运算较多地是采用扎德给出的定义:设
=∫(μA(u)/u)来表示U上的一个模糊子集A,当然,表示的方法还有许多,并且各有优点。模糊子集的运算较多地是采用扎德给出的定义:设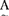 ,
,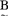 ∈F(U),定义
∈F(U),定义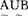 (并),
(并),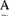 nB(交),
nB(交),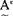 (余)分别具有下列隶属函数:
(余)分别具有下列隶属函数: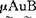 (u)
(u)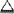 max(
max(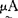 (u),
(u),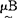 (u)),μAB(u)
(u)),μAB(u)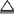 min(μA(u),
min(μA(u),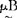 (u),
(u),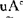
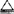 1-
1-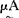 (u)。可以证明,普通集合运算的不少性质,对模糊集合也仍然适用。模糊数学从1965年发展至今,发展速度很快,应用的触角正伸向科技领域的许多方面。
(u)。可以证明,普通集合运算的不少性质,对模糊集合也仍然适用。模糊数学从1965年发展至今,发展速度很快,应用的触角正伸向科技领域的许多方面。
而作为模糊数学之基础的模糊子集自然有很大的作用,并占有很重要的地位。
- 岩心钻探工具手册是什么意思
- 岩性学是什么意思
- 岩惹惹木是什么意思
- 岩成土是什么意思
- 岩成土壤是什么意思
- 岩户景气是什么意思
- 岩房是什么意思
- 岩扁是什么意思
- 岩扉是什么意思
- 岩扉松径长寂寞,唯有幽人自来去。是什么意思
- 岩披宿雾三竿日,路引迷人四照花。是什么意思
- 岩拉是什么意思
- 岩旺湖电排站是什么意思
- 岩村是什么意思
- 岩杰可和岩萨特是什么意思
- 岩松义雄是什么意思
- 岩板儿是什么意思
- 岩板寨村落是什么意思
- 岩柏草是什么意思
- 岩栖是什么意思
- 岩栖之士岩穴之士是什么意思
- 岩栖干溪树,泽饮卑蹄涔。是什么意思
- 岩栖幽事是什么意思
- 岩栖穴处是什么意思
- 岩栖草堂是什么意思
- 岩栖谷隐是什么意思
- 岩栖谷饮是什么意思
- 岩株是什么意思
- 岩样是什么意思
- 岩根是什么意思
- 岩桂是什么意思
- 岩梦是什么意思
- 岩棉栽培是什么意思
- 岩棱是什么意思
- 岩棲高士图是什么意思
- 岩棺是什么意思
- 岩椒是什么意思
- 岩楹是什么意思
- 岩楼是什么意思
- 岩母斤是什么意思
- 岩母部是什么意思
- 岩江片是什么意思
- 岩江片的故事是什么意思
- 岩池是什么意思
- 岩汪湖电力排灌站是什么意思
- 岩泉是什么意思
- 岩泉上,飞凫浴;巢林下,栖禽宿。是什么意思
- 岩泉他夕梦,渔钓往年逢。是什么意思
- 岩泉山人是什么意思
- 岩泊渡工程是什么意思
- 岩波书店是什么意思
- 岩波日中辞典是什么意思
- 岩泽兰是什么意思
- 岩洞是什么意思
- 岩洞大棺葬是什么意思
- 岩洞小棺葬是什么意思
- 岩洞的美称是什么意思
- 岩洞露尸葬是什么意思
- 岩流溅、涎香惯搅,娇龙春睡。是什么意思
- 岩浅大神经是什么意思