模态逻辑

---

关于含有模态词“必然”、“可能”的模态命题及其推理的逻辑学科。

它的历史可以追溯到亚里士多德，但对它的现代研究开始于美国逻辑学家刘易斯(C．I．Lewis)，他把数理逻辑的方法引入模态逻辑的研究，是现代模态逻辑的创始人。

模态逻辑有模态命题逻辑和模态谓词逻辑。

模态命题逻辑的语言是古典命题逻辑语言的一个扩集，具体来说，它包括：

Ⅰ命题变项：p，q，r，s，p₁，q₁，r₁，s₁，…

Ⅱ逻辑联结词：，∧，∨，→，

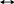
Ⅲ括号：(，)

Ⅳ模态词：□，◇

模态命题逻辑的公式是古典命题逻辑公式的一个扩集，其定义如下：

Ⅰ单个命题变项加左、右括号是公式，即(p)，(q)，……是公式；

Ⅱ如果(α)是公式，则(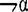)是公式；

Ⅲ如果(α)和(β)是公式，则(α∧β)、(α∨β)、(α→β)、(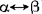)都是公式；

Ⅳ如果(α)是公式，则(□α)、(◇α)是公式；

V只有根据Ⅰ－Ⅳ形成的是公式。

模态命题逻辑的系统是在古典命题演算中引进模态词□与◇所构成的，除了它的语言和公式的定义作必要的扩充之外，还要引进包含模态词□与◇的公理与推理规则，证明与可证的概念与古典命题演算中类似，公式α在模态系统S中可证，仍称α为S的定理，证作。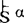

当把模态公式作为公理加到古典命题演算中去时，首先加入的是K公式：

K□(p→q)→(□p→□q)

由古典命题演算加K所构成的系统简称K系统，它是最小的模态命题系统。由K再加其他模态公式作为公理可以构成其他的模态命题逻辑系统，它们通称为正规模态命题逻辑系统。

一个正规模态命题S是所有古典命题逻辑重言式的一个扩集，扩集满足两个条件：

(1)□(p→q)→(□p→□q)∈S；

(2)S在分离规则、代入规则、必然化规则之下封闭。

K系统是最小的正规模态命题系统，所有其他模态命题逻辑都是由给K添加模态公式而得到的。兹列举一些常被作为不同的模态命题系统的公理的模态公式：

D(deontic)．□P→◇P

T(Feys，t)．□P→P

4(S4)．□P→□□P

E(Euclidean)．◇P→□◇P

B(Brower)．P→□◇P

Tr(trivial)．□P→P

Dum(Dummet)．□(□(P→□P)→P)→(◇□P→P)

由K分别添加D、T作为公理就分别得到正规命题逻辑系统KD、KT，简记为D、T。用这种办法，我们可以用以上列举的模态公式定义许多模态逻辑系统。兹举其中一批如下：

KT=T=哥德尔／费斯／冯·莱特的系统

KT4=S₄

KT4B=KT4E=S5

KD=道义逻辑系统T

KD4=道义逻辑系统S₄

KD4E=道义逻辑系统S₅

KTB=布劳维尔系统

KT4Dum=D=普赖尔的模态逻辑系统Q

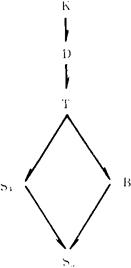
在这些系统中，常见的正规模态命题逻辑系统是K、D、T，S₄、S₅、B，它们之间具有一定的关系，例如K真包含于D，这就是说，K的定理都是D的定理，但D的定理并不一定是K的定理，我们用“K→D”表示，则上述几个常见系统之间的关系可以图示如下：

除了正规模态命题逻辑之外，还有非正规的模态命题逻辑。

模态谓词逻辑实际上是对于模态命题逻辑的一种扩充，也就是说，它是在后者的基础上，再加入一些新的语言、公式、公理和变形规则得到的。

例如，模态谓词逻辑的语言是模态命题语言的一个扩集，它包括：

1．模态命题逻辑语言Ⅰ一Ⅳ：

2．个体变项：μ，v，w，x，y，z，μ₁，v₁，w₁，…

3．谓词变项：F，G，H，P，Q，R，S，F₁，G₁，H₁，…

4．量词：，。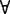

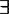相应地，模态谓词逻辑的公式是模态命题逻辑公式集的一个扩集，定义如下：

1．模态命题逻辑公式的定义Ⅰ一Ⅳ；

2．一谓词变项后继有写在一对括号内并用逗点分开的适当数目的个体变项是公式；

3．如果(α)是公式，并且x是一个体变项，则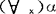、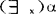是公式。

这里有必要提到著名的巴坎公式，记为BF：

BF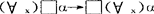

正规模态谓词逻辑是对正规模态命题逻辑(记为S)作必要的扩充之后得到的。我们可以定义一般形式的包含BF的正规模态谓词逻辑，记为S+BF。

S+BF有以下公理图式：

S．如果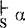并且α’是α的古典谓词逻辑的代入特例，则α’是S+BF的公理。(α’是α的古典谓词逻辑的代入特例，就是说，α’是用模态谓词逻辑的某些公式处处代换α中的每一命题变项而得到的。)

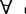如果α是任一公式，x和y是任一个体变项，则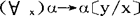是S+BF的公理(α中的x不在(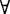y)的辖域内自由出现)。

BF 如果α是任一公式，并且x是任一个体变项，则(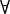x)□α→□(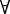x)α是S+BF的公理。

S+BF的变形规则除了分离规则和必然化规则外，还有：

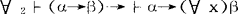(x不在α中自由出现)。

从这种一般形式出发，可以得到许多正规模态谓词逻辑系统，例如，T+BF，S₄+BF。应该指出，模态谓词逻辑的发展是很不成熟的，面临很多难题。

模态逻辑在不太严格的意义上构成了哲学逻辑的基础部分，它是理解其他许多哲学逻辑分支，例如时态逻辑、道义逻辑，认识论逻辑等等的前提条件。