14.1.1 概率的基本性质
❶ 0≤P(A)≤1,P(A)=1-P(A),A为任何事件。
❷ P(Ω)=1,P(Φ)=0,Ω、Φ分别表示必然事件和不可能事件。
❸ 若A、B互斥,则P(AUB)=P(A)+P(B)否则,P(AUB)=P(A)+P(B)-P(A∩B)
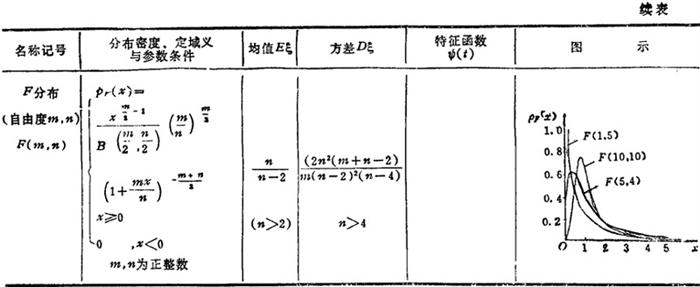
❹ 若A B,则P(A)≥P(B),且P(A)-P(B)=P(A\B)
B,则P(A)≥P(B),且P(A)-P(B)=P(A\B)
❺ 若A1,A2,…,An是两两互斥的事件完备组。则P(A1UA2U…UAn)==P(A1)+P(A2)+…十P(An)=114.1.2概率的计算公式
❶ 条件概率与乘法公式。在事件B发生的条件下,事件A发生的概率称为A在B已发生的条件下的条件概率,记作P(A|B),当P(B)>0时,规定
14.1.5 大数法则与中心极限定理
(1)大数法则
伯努利定理:随机事件A在n次独立试验中的频率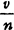 依概率收敛于事件A的概率ρ,即对任意e>0,
依概率收敛于事件A的概率ρ,即对任意e>0,
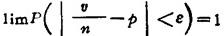
互相独立的随机变量ξ1,ξ2,…,如果(i)存在均值和方差,记作Eξk=μ,Dξk=σ2(k=1,2,…);或者(ii)具有相同分布,且有有限均值Eξk=μ,那么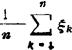 依概率收敛于随机变量的均值Eξk=μ,即对任意ε>0,
依概率收敛于随机变量的均值Eξk=μ,即对任意ε>0,
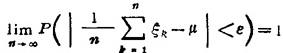
如果互相独立具有相同分布的随机变量ξ1,ξ2,…的均值和方差都存在,记Eξk=μ,Dξk=σ2
(k=1,2,…),那么
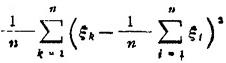
依概率收敛于随机变量的方差Dξk=σ2,即对任意ε>0,
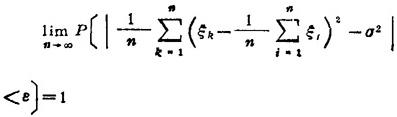
(2)中心极限定理
1)如果互相独立具有相同分布的随机变量ξ1,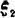 ,…的均值和方差都存在,记Eξk=μ,Dξk=σ2(k=1,2,…),那么随机变量
,…的均值和方差都存在,记Eξk=μ,Dξk=σ2(k=1,2,…),那么随机变量
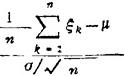
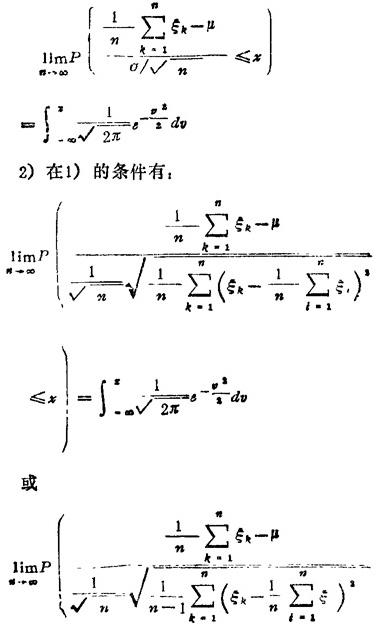
渐近地遵从标准正态分布N(0,1),即
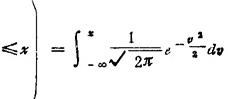
- 叶圣陶是什么意思
- 叶子是什么意思
- 叶子烟是什么意思
- 叶尼塞河是什么意思
- 叶序是什么意思
- 叶志超是什么意思
- 叶挺是什么意思
- 叶斑病是什么意思
- 叶枝是什么意思
- 叶柄是什么意思
- 叶永烈是什么意思
- 叶片是什么意思
- 叶猴是什么意思
- 叶红素是什么意思
- 叶绍钧是什么意思
- 叶绿体是什么意思
- 叶绿素是什么意思
- 叶肉是什么意思
- 叶脉是什么意思
- 叶腋是什么意思
- 叶舟是什么意思
- 叶芝是什么意思
- 叶芽是什么意思
- 叶落归根是什么意思
- 叶落知秋是什么意思
- 叶蜂是什么意思
- 叶蜡石是什么意思
- 叶蝉是什么意思
- 叶轮是什么意思
- 叶酸是什么意思
- 叶金是什么意思
- 叶面是什么意思
- 叶鞘是什么意思
- 叶韵是什么意思
- 叶飞是什么意思
- 叶黄素是什么意思
- 号是什么意思
- 号丧是什么意思
- 号令是什么意思
- 号兵是什么意思
- 央求是什么意思
- 央行是什么意思
- 央请是什么意思
- 夯是什么意思
- 夯土是什么意思
- 夯实是什么意思
- 夯机是什么意思
- 夯歌是什么意思
- 夯砣是什么意思
- 失是什么意思
- 失业是什么意思
- 失业保险是什么意思
- 失主是什么意思
- 失之东隅是什么意思
- 失之东隅,收之桑榆是什么意思
- 失之交臂是什么意思
- 失之毫厘,差之千里是什么意思
- 失之毫厘,谬以千里是什么意思
- 失事是什么意思
- 失仪是什么意思