最小最大定理

---

对于局中人P有m个可供选择的纯策略，Q有n个可供选择的纯策略，P的赢得矩阵是m行n列的矩阵B=(b_ij)(的二人零和对策)，设P的混合策略是概率向量p=(p₁，p₂，…，p_m)，Q的混合策略是概率向量q=(q₁，q₂，…，q_n)，因为p₁，p₂，…，p_m≥0，并且p₁+p₂+…+p_m=1，所以p在m－1维标准单纯形S^m－1={x=(x₁，…，x_m)|x₁，…，x_m≥0，x₁+…+x_m=1}上，同样，q在n－1维标准单纯形S^n－1={y=(y₁，…，y_n)|y₁，…，y_n≥0，y₁+…+y_n=1}上。

如果P选用混合策略p∈S^m－1，可以预料P的赢得至少是：

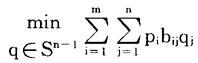
P的目标是选择p∈S^m－1使得他的“最小赢得”数即上式达到最大，也就是

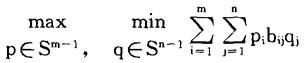
同样，Q的目标是选择q∈S^n－1使得P的“最大赢得”数

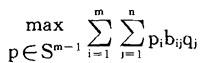
达到最小，也就是

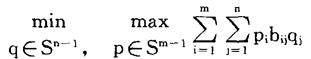
冯·诺依曼(Von Neumann)证明，一定成立

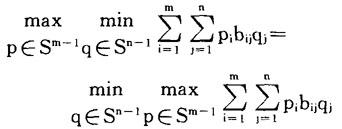
这就是二人零和对策的基本的最小最大定理，亦称鞍点定理。

这条定理目前已推广到比矩阵对策更一般的情形。