方差分量模型

---

在考虑具有随机效应的线性回归模型中，残差通常被认为由三部分组成：

v_it=α_i+λ_t+μ_it

其中，α_i表示变量的与时间无关的固定效应，λ_t表示仅与时间有关的效应，μ_it表示任一变量特定的与时间有关的效应作为随机变量，α_i，λ_t，μ_it满足以下性质：

Eα_i=Eλ_t=Eμ_it=0，

Eα_iλ_t=Eα_iμ_it=Eλ_tμ_it=0，

Eα_iα_j=σ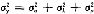，如果i=j；

=0，如果i≠j

Eλ_tλ_s=σ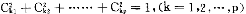 如果t=s，

=0，其他

Eμ_itμ_js=σ# 如果i=j，t=s；

=0，其他

而且

Eα_Ix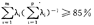_t=Eλ_tx_i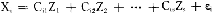t=Eμ#_t=0

这时因变量的方差由三部分组成，即

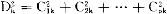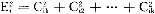σ=σ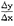+σ+σ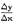

这三个分量都叫方差分量，相应的模型

y_it=β′x_it+v_it

叫方差分量模型