数列的表示方法

---

从函数的观点看，数列的表示方法有如下三种：

(1)解析法：用通项公式或其他式子表示数列；

(2)列表法：数列可以看作是列表法给出的函数(定义域为正自然数集，或它的有限子集{1，2…n})，自变量省略，只列出函数值；

(3)图象法：数列可以用图形(一群孤立的点)来表示．

利用数列的通项a_n求数列的最大项或最小项，

若求最大项a_n，则a_n满足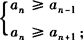；若求最小项a_n则a_n满足．

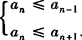例1 根据下列数列前n项的值，写出数列的一个通项公式．

解 (1)把数列的前n项写成

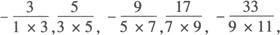
由于数列的各项正、负交替出现，因此每项都有一个因子(—1)ⁿ，

又分子构成的规律可记为2ⁿ+1，分母为两个连续奇数的积，

∴通项公式为：

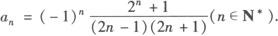
(2)数列9，99，999，…，前几项可以写成10—1，10²—1，10³—1，…，

∴通项公式为：

a_n=10ⁿ—1(n∈N^*)．

∴数列的通项公式为

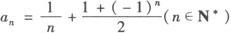
例2 已知下面各数列{a_n}的前n项和S_n的公式，求{a_n}的通项公式．

(1)S_n=2n²—3n；

(2)S_n=3ⁿ—2．

解 (1)a₁=S₁=—1．

当n≥2时，a_n=S_n—S_n1

=(2n²—3n)—[2(n—1)²—3(n—1)]

=4n—5

由于a₁也适合此等式，

∴a_n=4n—5(n∈N^*)．

(2)n=1时，a₁=S₁=1．

当n≥2时，a_n=S_n—S_n—1=2·3^n—1．

由于a₁不适合此等式，