效用函数

---

对消费集X上的一个消费者偏好关系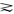，如果存在一个X上的函数u(·)满足性质：对任何x，y∈X，u(x)＞u(y)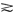x＞y，u(x)=u(y)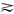x～y，u(x)≧u(y)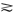x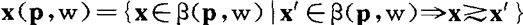y，则称u(·)为表示偏好关系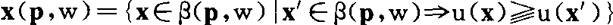的效用函数。

对一个偏好关系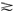是否存在表示它的效用函数，是一个长期争论的问题。1954年德布鲁(Debreu)证明：

若偏好关系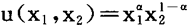满足完全性、自返性、传递性和连续性这四个假设时，必存在一个表示它的连续效用函数。

当存在表示偏好关系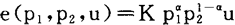的效用函数u(·)时，消费者的需求定义

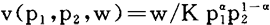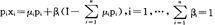x(p，w)={x∈β(p，w)|x′∈β(p，w)xx′}

就等价于

x(p，w)={x∈β(p，w)|x′∈β(p，w)#u(x)≧u(x′)}