操作手的雅可比矩阵

---

(Jacobian)

操作手运动学的正问题和逆问题，从正反二方面研究了关节状态矢量与末端装置的位置与方位之间的关系。在运动控制中，尚需确定关节的无穷小运动在末端装置位置与方位无穷小变化之间的关系。在无穷小关节运动与无穷小末端装置运动之间存在一线性关系。这一关系可用雅可比矩阵定义。若设末端装置的微小移动和微小转动为d和δ，则

j关节转动对末端装置角速度Ω的奉献为

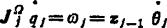
(5．13-43)

总起来，如果j关节为转动关节，则

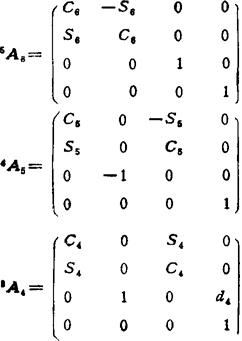
由于关节2和3的轴是平行的，可用¹A₃=¹A₂²A₃代替¹A₃和，故需要计算的矩阵为：

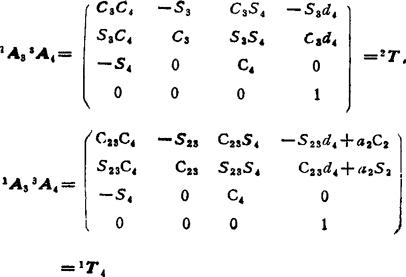
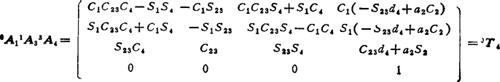
从以上各式中即可得到式(5．13-53)和(5．13-54)的各变量。因为

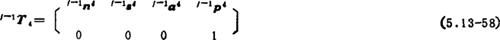
由(5．13-53)式计算操作手雅可比矩阵各列，得

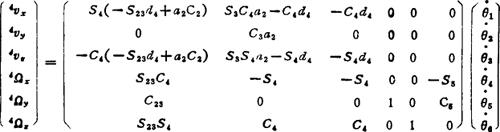
雅可比矩阵元素中有重复项，上式等价于

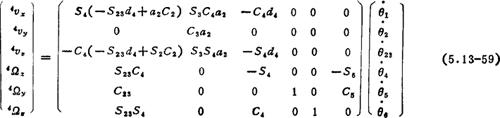
式中θ₂₃=θ₂+θ₃。由(5．13-57)式计算⁴n、⁴a⁴a和⁴p，得

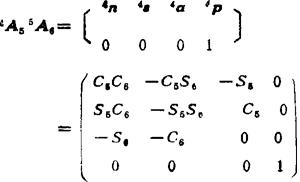
由(5．13-56)式得

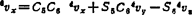
6v_y=－C₅S₆⁴v₂－S₅S₆⁴v_y－C₆⁴v₂

6v₂=-S₅4v_x+C₅4v_y

6Ω_x=C₅C₆⁴Ω₂+S₅C₆⁴Ω_y-S₆⁴Ω₂

6Ω_y=－C₅S6^＇Ω₂－S₅S₆4Ω_y－C₆4Ω₂

6Ω₂=－S₅⁴Ω_x+C₅4Ω_y

计算⁴J只需11次乘法运算和3次加法运算；求⁴v和⁴Ω需要16次乘法运算和12次加法运算；求⁶v和⁶Ω需要20次乘法运算和10次加法运算。总数分别为47次和25次。