阶的估计的重要方法。
该方法主要是对形如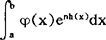 的积分进行估计,当x→+∞时,无穷大量ex的增长速度是“相当快”的,因此,如果函数h(x)在(a,b)中某一点x0达到最大值,那么,由于h(x0)-h(x)>0,当n→∞时,en(h(x0)-h(x))的增长也是相当快的,也就是说,对于x0的任一邻域外的x值,enh(x)相对于enh(x0)是可以忽略不计的,这就是拉普拉斯方法的基本思想。
的积分进行估计,当x→+∞时,无穷大量ex的增长速度是“相当快”的,因此,如果函数h(x)在(a,b)中某一点x0达到最大值,那么,由于h(x0)-h(x)>0,当n→∞时,en(h(x0)-h(x))的增长也是相当快的,也就是说,对于x0的任一邻域外的x值,enh(x)相对于enh(x0)是可以忽略不计的,这就是拉普拉斯方法的基本思想。
拉普拉斯方法有著极其广泛的应用,它的核心就是以下的重要定理。
定理1(拉普拉斯)设φ(x)与h(x)在〔a,b〕上有定义,且满足条件:
(1)对于任意的n≥n0,φ(x)enh(x)在〔a,b〕上可积;
(2)h(x)在〔a,b〕上只有一个最大值点x=ξ,ξ∈(a,b),而且在任何不包含ξ的闭区间(α,β〕内,有supx∈〔α,β〕 h(x) (3)在ξ的某一邻域内,h”(x)连续,h”(ξ)<0; (4)φ(ξ)≠0,φ(x)在x=ξ连续, 则当n→∞时,有 显然,当a或b为∞时,只要|φ(x)enh(x)|(n≥n0)在相应的无穷区间上可积,则定理1仍然成立,作为定理1的应用,容易推得重要的斯特林公式:因为 对于在端点达到最大值的情形,类似地可以得到下面的定理。 定理2,设φ(x)与h(x)在〔a,b〕上有定义,且满足: (1)对于任意整数n≥n0,φ(x)enh(x)在〔a,b〕上可积 (2)h(x)在x=a达到最大值且对任何区间〔α,b〕(α>a),都有 (3)存在η>0,使得h”(x)与Φ(x)在〔a,a+η〕内连续; (4)h’(a)=0,h”(a)<0,φ(a)≠0, 则当n→∞时,有 对于h’(a)≠0或h’(b)≠0的情形,亦有类似的结果。 作为定理2的应用,下面来研究重要的n阶贝塞尔函数 φ(θ)=cosnθ,h(θ)=cosθ,a=0, 则立即可得到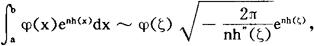
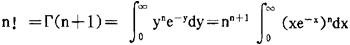 ,若取
,若取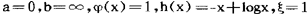 ,由定理1可得
,由定理1可得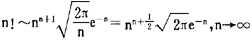 。这就是斯特林公式。
。这就是斯特林公式。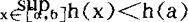 ;
;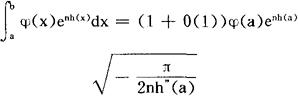
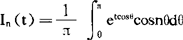 当t→∞时的阶,在定理2中,取
当t→∞时的阶,在定理2中,取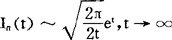 。
。
- 黑龙江省旅游事业局是什么意思
- 黑龙江省旅游产品生产供应公司是什么意思
- 黑龙江省旅游局是什么意思
- 黑龙江省旅游汽车公司是什么意思
- 黑龙江省旅游管理条例是什么意思
- 黑龙江省旅游质量监督管理所是什么意思
- 黑龙江省朝鲜语学会是什么意思
- 黑龙江省植物志是什么意思
- 黑龙江省民族博物馆是什么意思
- 黑龙江省民族研究学会是什么意思
- 黑龙江省沿岸的部落是什么意思
- 黑龙江省消费者协会是什么意思
- 黑龙江省渤海上京遗址博物馆是什么意思
- 黑龙江省现行事业行政经费开支规定手册是什么意思
- 黑龙江省电力旅行社是什么意思
- 黑龙江省畜牧兽医学校是什么意思
- 黑龙江省社会科学学会联合会是什么意思
- 黑龙江省科学技术协会是什么意思
- 黑龙江省红楼梦学会是什么意思
- 黑龙江省绥化地区科技精英是什么意思
- 黑龙江省绥棱县兴奇木制品厂是什么意思
- 黑龙江省美术馆是什么意思
- 黑龙江省群众文化学会是什么意思
- 黑龙江省翻译工作者协会是什么意思
- 黑龙江省艺术学会是什么意思
- 黑龙江省艺术学校是什么意思
- 黑龙江省花园村旅行社是什么意思
- 黑龙江省蒙古语文学会是什么意思
- 黑龙江省蕨类植物是什么意思
- 黑龙江省蚕业研究所是什么意思
- 黑龙江省行政区划简册是什么意思
- 黑龙江省西部草原常见植物检索是什么意思
- 黑龙江省证券公司是什么意思
- 黑龙江省评剧团是什么意思
- 黑龙江省诗书画院是什么意思
- 黑龙江省语言学会是什么意思
- 黑龙江省财政年鉴是什么意思
- 黑龙江省财政沿革利弊说明书是什么意思
- 黑龙江省达斡尔族学会是什么意思
- 黑龙江省通信公司是什么意思
- 黑龙江省遥感矿化蚀变信息提取方法研究是什么意思
- 黑龙江省邮政储汇局是什么意思
- 黑龙江省邮政实业集团公司是什么意思
- 黑龙江省邮政局是什么意思
- 黑龙江省邮政易通物流有限责任公司是什么意思
- 黑龙江省邮政速递局是什么意思
- 黑龙江省鄂温克族研究会是什么意思
- 黑龙江省野生动物名录是什么意思
- 黑龙江省金融业名录大全是什么意思
- 黑龙江省钱币学会是什么意思
- 黑龙江省铁路公司购地合同是什么意思
- 黑龙江省镜泊湖风景名胜区管理规定是什么意思
- 黑龙江省革命博物馆是什么意思
- 黑龙江省鸟类志是什么意思
- 黑龙江省黑河区鄂伦春协领公署印是什么意思
- 黑龙江省黑龙江及乌苏里江地区经济地理是什么意思
- 黑龙江省(哈尔滨市)是什么意思
- 黑龙江省(黑)是什么意思
- 黑龙江科学技术出版社是什么意思
- 黑龙江移动通信有限责任公司是什么意思