投影界及极小投影理论

---

投影概念原始出自几何。

自空间及映射概念拓广以来，投影P乃代表一种映射，由空间X映到一子集M上，合P2=P。又分线性与非线性两大类，前者是线性投影(寻常只称投影)，所指P是线性连续的。

而M是个余子空间。另一类乃度量投影，即度量空间中点到一个集的近距映射，一般是非线性的。

早在1940年R．S．Philips及1941年A．Sobczyk已发现Co及c都是l^∞中非余的闭子空间(即线性投影不存在)。1971年Lindenstrauss和TzafriIi发现M［0，1］中C［0，1］也是非余的，并发现凡B空间中要使任一闭子空间都是余的必须只须它同构于Hilbert空间。

幸好赋范空间中的有限维子空间总是余的，于是人们最感兴趣是到有限维子空间M的投影，一般M上投影两大问题是投影极小范数λ(M)=inf｛‖P‖：P投影到M｝及极小投影P₀，即‖P₀‖=λ(M)，是否存在及构造如何。余子空间M是个共轭空间时，M上极小投影存在。

Berman－Harschiladze(1940)最早证出C［a，b］到n次多项式空间π_n投影极小范数λ≥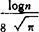。但极小投影构造始终未能给出。到1990年K．Petras把λ值必进到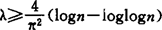。富里车贝展式部分和只是渐近地到达极小范数。

1986年P．Vertesi讨论了离散化成的Lewanowic算子。但也指出要求内插性的渐近极小投影是不存在的。除非λ(M)=1情形。对于周期函数情形即顺利得多，Lozinski1948年证明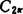到n阶三角多项式空间T_n的富里和是极小投影。

1969年Cheney、Hobby、Morris、Wulbert和Schurer的论文又证实是唯一极小投影。1978年，C．Franchetti和Cheney证明L²［0，1］中Rademacher投影是极小投影，而冯玉瑜考虑Walsh投的极小性。一般B空间说对n维M，λ(M)能有多大界限?对此1971年M．Kadec和Snober证明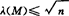，且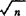是最佳数。一方面1941年Sobczyk在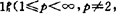n维)中找到子空间M，使。

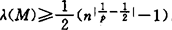1960年B．Grünbaum找到了1¹到ψ^－1(0)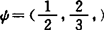，…)的λ=2，但不存在极小投影。1976年C．Franchetti和Cheney算出了L¹［－1，1］到二维子空间π1则λ(πj)≈1．2204对Disc代数A(D)到π_n则1975年K．O．Geddes和T．C．Masan证出Taylor投影是极小投影。

继之1982年Fisher、Morris和Wulbert证明唯一极小性。1982年L．Brutman算出λ渐近数值量阶为logn，一些非极小投影范数又能多大呢?1973年J．W．Baker证明C空间中Sup｛‖P‖：P投影到n维M｝≥2n+1，表明投影界数值分布的宽广性。

特殊结构的投影如插值投影，则联系著Turan最优结理论，80年代Kilgoor，Bor，Pinkus和Brutman等人颇多研究；还有积分形算子投影研究亦颇受注意。对超平面H的极小投影问题，首先1≤λ(H)≤2。

1983年Franchetti考究确有没有投影到H上的P，使‖P‖≤2呢?他获知一个充分条件乃是H中任何有界集都存在车贝中心。

特别设X^{* *}到X有范数1投影(更特别是，X自反)则充分合。

1986年S．Rolewiez研究LP［0，1］中到超平面极小投影。因为自反空间中，对凡余子空间极小投影必存在。

1983～1984年W．L．Odinez进一步考究极小投影唯一性，指出自反严凸空间中，对超平面极小投影若‖P‖＞1则P是唯一极小投影。又由Lindenstrauss1966年关于自反空间可改等价范数成光滑严凸的命题，用此推到B，空间总可改等价范数使到任何超平面的极小投影是唯一的。

范数1投影当然是更特殊的极小投影，但除非Hilbert空间，它不会遍布出现。早在1939年S．Kakutani已发现三维X中若到任何二维子空间都有范数1线性投影，则X只能是Hilbert空间。

不过凡赋范空间中到一维子空间必存在范数1投影。二维情形就很不同。

范数1投影一基本问题是什么X，什么余子空间M才保证X到M范数1投影存在呢?还未系统解决。1966年T．Ando发现L^p［0，1］(1≤P≤∞，p≠2)中对闭超平面不存在范数1投影。

L1^{* *}［0，1］到L1［0，1］则有范数1投影。

1977年B．Beauzamy和B．Maurey继续此研究，考究扩大的空间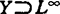(μ)，1984年已获知Y到L^∞(μ)有范数1投影。但L^∞换为一个光滑空间X则否定，1971年Lindenstrauss和Wulbert指出C(Q)中到M有范数1极小投影的特征。若任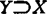，都存在Y到X的范数1投影，X就叫(P₁)空间。

类似用‖P‖≤λ相应叫(P_λ)空间。1950年D．B．Goodner指出了(P₁)空间一些等价条件，一定程度等距同构于C(Q)、Q极端不连通。至于E．M．Alfsen和E．G．Effros1972年L^P投影理论蓬勃发展以来，那些LP投影均是范数1投影。

L^P和块，M伊等都是1余子空间。

非线性大类以度量投影P_G为代表与线性投影大异，其界总有1≤‖P_G‖≤2。界与P_GLip性或Lip选都有关联。

1958年G．Freud著名命题强唯一性推局部Lip性。严凸空间中从R半径闭球入手易证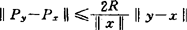。所以是局部Lip的。1975年O．Bjornestal及1983年T．Abatzoglou证出一致凸且一致光滑空间中，对闭凸集G，则PG是一致Lip的，且给出‖P_Gy－P_Gx‖的上界，用凸模反函数δ^－1与光滑模ρ表示。关于‖PG‖界限，1980年F．Deutsch和J．M．Lambert找出了C［0，1］中到达‖P_G‖=2的例子。还有任指定1≤γ≤2，在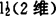中找到1维车贝子空间G，使‖P_G‖=2，且P_G线性。

1980年P．D．Morris也有P_G线性例。可见度量投影具线性及‖P_G‖=1都不限于Hilbert空间所独有。

标志著空间结构一个重要常数是射径Lip常数∧(X)。命T是对单位球度量投影(叫射径投影)，即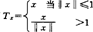1967年Figueiredo和Karlovitz已指出T是一致Lip的，‖T_rT_y‖≤λ‖x－y‖。如此λ的最小值称X的射径Lip常数。1≤∧(X)≤2，在1974年R．L．Thele的一个计算∧(X)公式基础上，1983年P．Kapoor和S．B．Mathur证实了一个重要关系∧(X)=MPB(X)，即∧(X)与空间的度量投影界同值，从而使MPB(X)数值计算上有了简化途径。

已求出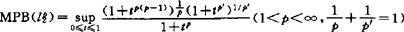特别地p=3，4相应值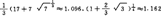。补充一下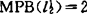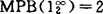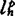，，，情形还未推出。

1980年Franchetti证实B．空间有∧(X)=∧(X^*)．∧(X)实质上与B．空间的其他常数有内在联系，对于了解空间结构有相当作用。

例如，M．A．Smith证明了MPB(X)＜2等价于X是NQ(匀非方)空间。

。【参考文献】：

1 Sobczyk A. Duke M J,1941, 8,78～106

2 Grunbaum B. Pac,J M,1960,10:193～201

3 Cheney C A, Hobby P. Tran AM S.1969.1:249～258

4 Baker J W. Appr Theory I,Texas 1973.247～250

5 Cheney C E W. Spaces, Appr, Theory I ,Texas, 1976,365～368

6 Deutsch F.Lambert J M. JAT, 1980,29(2) :116～131

7 Franchetti C. JAT ,1983,38t319～333

8 Kapoor P,Mathur S B. JAT,1983,38:66～70

9 潘文熙，数学季刊，1989，4(2)∶39～46．

(暨南大学潘文熙教授撰)