总体分布的估计

---

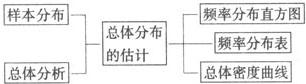
利用样本的累积频率分布图，可以对总体的相应情况进行估计，当样本容量无限增大，分组组距无限缩小时，频率分布直方图就会趋近于一条光滑曲线——总体密度曲线，相应地，累积频率分布图也会趋近于一条光滑曲线——累积频率分布曲线，如图，它反映了总体的累积分布规律，即曲线上任意一点P(a，b)的纵坐标b，表示总体取小于a的值的概率．

1．若总体密度曲线就是或近似地是函数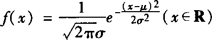的图象，则其分布叫正态分布，常记作N(μ，σ²)，其中μ，σ(σ>0)分别表示总体的平均数与标准差．f(x)的图象称为正态曲线．

2．正态曲线具有两头低、中间高、左右对称的基本特征．

正态曲线具有以下性质：

(1)曲线在x轴上方，与x轴不相交．

(2)曲线关于直线x=μ对称．

(3)曲线在x=μ时位于最高点

(4)当x<μ时曲线上升；当x>μ时，曲线下降，并且当曲线向左、右两边无限延伸时，以x轴为渐近线，向它无限靠近．

(5)当μ一定时，曲线的形状由σ确定，σ越大，曲线越矮胖，表示总体的分布越分散；σ越小，曲线越瘦高，表示总体的分布越集中．

3．函数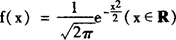的图象称为标准正态曲线．

当μ=0，σ=1时，正态总体称为标准正态总体，记作N(0、1)．

4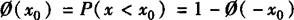．标准正态总体在任一区间(x₁，x₂)内取值的概率．

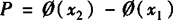5．对任一正态总体N(μ，σ²)，取值小于x的概率．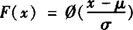

例1 下列函数是正态密度函数的是( )．

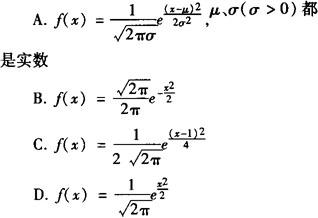
解 仔细对照正态分布密度函数f(x)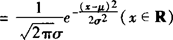，注意指数上的部分的σ和系数的分母上σ要一致，以及指数部分是一个负数．

A错在正确的函数的系数分母的二次根式不包含σ的，而且指数部分的符号应当是负的，B是正态分布N(0，1)的密度分布函数，C对照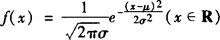，从系数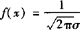看σ=2，可是从指数部分看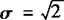，不正确，D错在指数部分缺少一个负号，∴应选B．

我们一定要小心识别各种函数是不是正态分布密度函数，不能貌似相似就认定是正态分布密度函数．

例2 关于正态曲线性质的叙述：

(1)曲线关于直线x=μ对称，这个曲线在x轴上方．

(2)曲线关于直线x=σ对称，这个曲线只有当x∈(—3σ，3σ)时才在x轴上方．

(3)曲线关于y轴对称，因为曲线对应的正态密度函数是一个偶函数．

(4)曲线在x=μ时处于最高点，由这一点向左右两边延伸时，曲线逐渐降低．

(5)曲线的对称轴由μ确定，曲线的形状由σ确定．

(6)σ越大，曲线越“矮胖”，σ越小，曲线越“瘦高”．

上述说法正确的是( )．

A．只有(1)(4)(5)(6)

B．只有(2)(4)(5)

C．只有(3)(4)(5)(6)

D．只有(1)(5)(6)

解正态曲线是一条关于直线x=μ对称，在x=μ时处于最高点并由该点向左右两边延伸逐渐降低的曲线，该曲线总是位于x轴上方，曲线的形状由σ确定，而且比较若干不同的σ对应的正态曲线，可以发现σ越大，曲线越“矮胖”，σ越小，曲线越“高瘦”．答案是A．

正态曲线的这些简单性质是要熟练掌握并且能够应用的，尤其是对称性、最高点的位置、曲线向横轴左右无限延伸时逐渐降低．

例3 设连续型随机变量ξ～N(μ，σ²)，则其密度函数P(x)的最大值为＿＿．

解 由于ξ～N(μ，σ²)，所以其密度函数为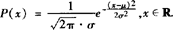．从而根据性质：曲线关于x=μ，并且在x=μ处达到最高点，即P(x)的最大值是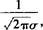答案为

．

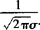例4 求使得下列各式成立的x

(1)Φ(x)=0．5；

(2)Φ(x)=0．95；

(3)Φ(x)=0．10．

解 (1)x=0；

(2)由于Φ(1．64)=0．9495，

Φ(1．65)=0．9505，所以取x≈1．64；

(3)由于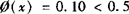，所以x<0，而Φ(x)=1—Φ(—x)，所以

Φ(—x)=0．90，

由于Φ(1．28)=0．8997，

Φ(1．29)=0．9015．

故取—x≈1．28，x=—1．28．

相关关系 自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系，与函数关系不同，相关关系是一种非确定性关系．

回归分析 对具有相关关系的两个变量进行统计分析的方法叫回归分析．

散点图 表示具有相关关系的两个变量的一组数据的图形叫做散点图．

回归直线方程，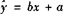

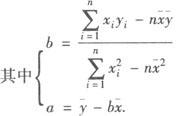
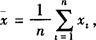，相应的直线叫做回归直线，对两个变量所进行的上述统计分析叫做线性回归分析．

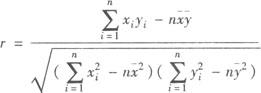
叫做变量y与x之间的相关系数．

例 下列两个变量之间的关系哪个不是函数关系( )．

A．角度和它的余弦值

B．正方形边长和面积

C．正n边形的边数和顶点角度之和

D．人的年龄和身高

解 函数关系就是一种变量之间有确定性的关系．A、B、C都是函数关系，甚至可以写出它们的函数表达式为f(θ)=cosθ，g(a)=a²，h(n)=nπ—2π．

D不是函数关系，对于年龄确定的人群，仍可以有不同身高的人，故应选择D．

函数关系未必都能写出函数表达式，例如对于自变量n，因变量为不超过n的素数的个数．