德宾－沃森检验

---

简称D－W检验，是检验扰动项是否存在一阶自相关的方法。

由于经济计量模型的自相关大多数是一阶自相关的情况，所以一般把D－W检验作为必要检验，其检验结果常与模型及其他必要检验的结果一起列出。

在D－W检验中，检验统计量称为d统计量(或D－W统计量)，定义如下：

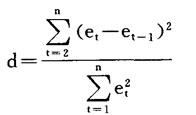
此处e_t=Y_t－Y_t(t=1，2，…，n)，是对模型应用普通最小二乘法所得的残差项。

可以证明，当样本容量n较大时，d≈2(1－#)，其中#为扰动项一阶自相关系数的估计量。

所以，当d=2时，#=0，扰动项不存在一阶自相关；d=0时，#=1，扰动项存在完全的一阶正自相关；d=4时，#=－1，扰动项存在完全的一阶负自相关。

由此可见，d统计量通常在0～4的范围内取值，当扰动项不存在一阶自相关时，d取值在2左右。

d统计量检验表给出上限d_U和下限d_L，当

d＜d_L时，扰动项存在一阶正自相关；

d_L＜d＜d_U时，不能确定；

d_U＜d＜4－d_U时，扰动项不存在一阶自相关；

4－d_U＜d＜4－d_L时，不能确定；

d＞4－d_L时，扰动项存在负自相关。

注意：(1)计算d统计量时，回归模型必须有截距项，以保证∑e_t=0。如果是无截距项的模型，就必须把截距项包括在内重新计算；

(2)解释变量必须是非随机变量；

(3)D－W检验正常只表示扰动项不存在一阶自相关，但仍有可能存在其他形式的自相关。