弹流润滑

---

弹流润滑(弹性流体动压润滑)自DowSonHigginson(1959)首次成功的运用逆解法获得弹流的完全数值解以来，发展十分迅速，在理论研究上已初步解决了从等温到非等温、从光滑表面到粗糙表面、从牛顿流到非牛顿流、从稳态到非稳态的过渡；在解决工程实际问题方面，也已在一些领域中建立了若干简化的公式和积累了一定数量的参考数据。

弹流润滑主要是解决异曲表面接触的摩擦和润滑问题。这种接触的特点是，接触面积很小而接触压力甚高(＞1GPa)。在这种条件下，局部的弹性变形达到和膜厚相同甚至更高的数量级，因此，在求解膜厚时必须考虑弹性变形。另外，润滑剂的流变性能将有质的变化，这将极大的影响润滑膜形状，压力分布、温度分布和牵曳力。

5．3．1 弹流润滑的基本理论

(1)Dowson及Higginsson的线弹流解

几何关系；如图1．5－17所示，弹性圆柱接触时，任意点x处的油膜厚度可表示为

粘压关系，当Hertz压力小于0．2GPa时，可用Barus方程

μ=μ₀e^ap (1．5－21)

式中 a为粘压系数，μ为压力为p时油的粘度；p为所受压力；μ₀为大气压下油的粘度。

密度与压力的关系：实验证明，

根据弹性力学理论，求得任意点x处的纵向弹性位移：

R－刚性，E－弹性，I－等粘度，V－变粘度

为了构成分域图，运用了以下新参量。粘性参量gv；

(4)椭圆接触润滑状态分域图和线接触一样，首先确定坐标参量；

5．3．2 弹流的工程应用

目前，弹流的基本知识已达到工程实用的阶段。例如利用H、S、Cheng关于椭圆接触的Grubin解，并将线接触膜厚计算公式简化为：

(3)凸轮挺杆副的膜厚计算

h=4．35×10^－3〔Lρn〕^0．74〔fN^0．74R^′0．26〕 (1．5－45)

式中 n为凸轮轴转速，r／min；L_ρ为润滑参数；f_N为挺杆接触参数，滑动接触挺杆取为l，滚动接触挺杆取为2l；l－接触点到轴中心的最短距离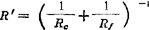；¹，其中R_c为接触点处的凸轮曲率半径；Rf为运动方向的挺杆半径(对平板凸轮)。

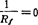(4)进口剪切热

上述计算膜厚h的公式，都是以弹流的等温解为基础的，事实上，当滚动速度较高或润滑剂粘度较大时，进口处的剪切热不应忽略不计(该热量提高了油温，从而减小了膜厚)。因此，当按前面的公式计算膜厚时，应乘以因子C_T来考虑剪切热的影响，C_T的值可查图1．5－25及图1．5－26。

(5)贫油

接触处润滑剂的供应并不总是充分的。为了考虑供油不足的影响，可将膜厚计算值乘一小于1的系数。根据Dowson等的研究，贫油效应达到平衡状态时，大概只有富油时膜厚的70%。故对中速或高速的轴承、齿轮和凸轮，在计算膜厚时在前面乘以0．7即可。

(6)非牛顿特性影响

在弹流接触的进口处剪切率甚高，很多流体，特别是高分子量流体和添加粘温指数增强剂的润滑剂，常表现出某些非牛顿特征。此时，决定膜厚的是在高剪切率下的粘度，而不是常规的低剪切率下的粘度。