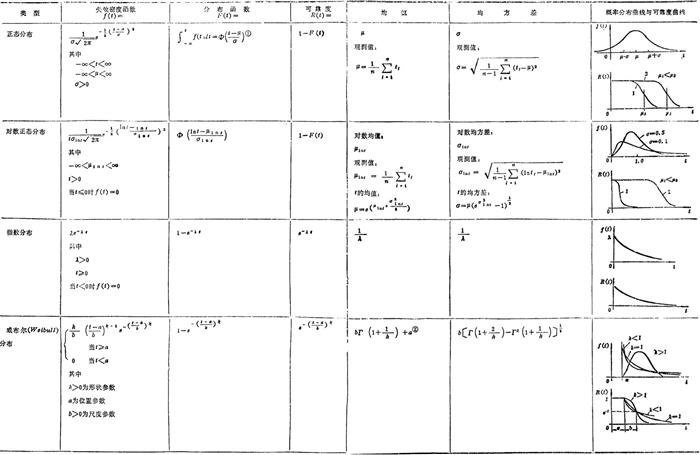
见表3.3-2、3、4。
表3.3-2 离散型随机变量概率分布
注:
❶ Φ( )为标准正态分布的累积分布函数,其值可由其函数表查得,见表3.3-7。
❷ Γ( )为Γ函数,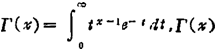 的值可查数学手册Γ函数表。
的值可查数学手册Γ函数表。
❸ 求失效率λ(t),可按λ(t)=f(t)/R(t)。
表3.3-4 常用分布的寿命公式

注:表中各符号含义见表3.3-3。
例3.3-1 某车间使用5台设备,已知设备在800小时内的失效概率为0.05,试求至少有3台在800小时内能正常工作的概率。
解:设各设备的失效事件互为独立,按二项分布,且设X为不能正常工作的设备数,由表3.3-2中公式
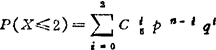
= ×0.955×0.050+
×0.955×0.050+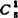 ×0.954×0.051+
×0.954×0.051+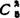 ×0.953×0.052=0.9988
×0.953×0.052=0.9988
例3.3-2 已知某飞机零件的寿命遵从威布尔分布,并已知形状参数k=2,位置参数a=0,尺度参数b=200h,试求当t=150h时的可靠度R(t),以及平均寿命和可靠度R=95%的可靠寿命。
解:由表3.3-3和3.3-4所列公式
可靠度:R(t)=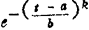 则
则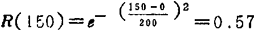
平均寿命: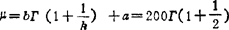 +0=177.2h,[Γ(1.5)=0.886,由Γ函数表查出]。
+0=177.2h,[Γ(1.5)=0.886,由Γ函数表查出]。
R=0.95的可靠寿命:t0.95=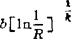 +α=
+α=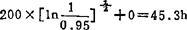
例3.3-3 已知齿轮寿命遵从对数正态分布,对数寿命的均值和均方差μlnt=14.506,σlnt=0.322,求平均寿命、寿命均方差、中位寿命、R=0.99的可靠寿命以及可靠度R(106)。
解:由表3.3-4所列公式
平均寿命:
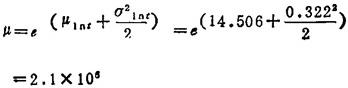
寿命均方差: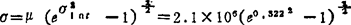
=0.69×106
中位寿命:t0.5=eμlnt=e14.506=2.0×106
R=0.99的可靠寿命:l0.59=e[μlnt+σlntΦ-1(1-R)]
=e[14.506+0.322Φ-1(1-0.99)]
=e[14.506+0.322(-2.326)]=0.94×106
可靠度:
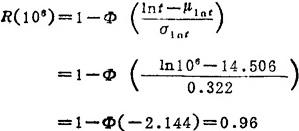
- 思想实验方法是什么意思
- 思想家和政委是什么意思
- 思想家:当代哲学的创造者们是什么意思
- 思想对行为的作用是什么意思
- 思想小结法是什么意思
- 思想工作是什么意思
- 思想工作是什么意思
- 思想工作和现代化是什么意思
- 思想工作心理学是什么意思
- 思想工作效率的社会学研究是什么意思
- 思想工作的艺术是什么意思
- 思想库是什么意思
- 思想库是什么意思
- 思想库是什么意思
- 思想库是什么意思
- 思想库是什么意思
- 思想库是什么意思
- 思想库是什么意思
- 思想建党是什么意思
- 思想建设是什么意思
- 思想建设是什么意思
- 思想建设是什么意思
- 思想建设是什么意思
- 思想录是什么意思
- 思想录 论宗教和其他主题的思想是什么意思
- 思想性是什么意思
- 思想性是什么意思
- 思想性是什么意思
- 思想性和科学性统一原则是什么意思
- 思想总结是什么意思
- 思想情操是什么意思
- 思想意识是什么意思
- 思想意识是什么意思
- 思想意识是什么意思
- 思想意识修养是什么意思
- 思想感情是什么意思
- 思想战线是什么意思
- 思想战线工作是什么意思
- 思想战线问题座谈会是什么意思
- 思想战线领导的涣散软弱状态是什么意思
- 思想挫折是什么意思
- 思想改造是什么意思
- 思想改造是什么意思
- 思想改造是什么意思
- 思想政治上和中央保持一致是什么意思
- 思想政治工作是什么意思
- 思想政治工作是什么意思
- 思想政治工作是什么意思
- 思想政治工作是什么意思
- 思想政治工作是什么意思
- 思想政治工作是什么意思
- 思想政治工作是什么意思
- 思想政治工作是什么意思
- 思想政治工作是什么意思
- 思想政治工作“万能”论是什么意思
- 思想政治工作“无用”论是什么意思
- 思想政治工作与业务工作相结合的原则是什么意思
- 思想政治工作与人际关系学是什么意思
- 思想政治工作与伦理学是什么意思
- 思想政治工作与文学是什么意思