岩体流变学

---

是流变学在岩体和岩石天然材料中的一个应用，是流变学的一个分支，它研究各种岩石(岩体)材料的变形及强度与应力、温度及时间的关系。

岩体或岩石的流变性是指岩石(体)的应力和变形随时间的变化过程，它包括蠕变与松驰两方面。

岩体流变问题研究的先驱是A．A．Michelson(1917)。

嗣后，R．H．Evans(1937)、D．T．Griggs(1939)等分别进行不同岩石材料的流变试验。

60年代开始，岩体流变学才引起普遍注意。中国算是开展岩石流变学理论研究较早的国家之一。早在50年代，结合三峡水利枢纽地下工程的特点，陈宗基提出了岩石流变概念及其有关理论。

从70年代后期起，他在中科院地球物理所，致力于运用流变学研究大地的变迁，并研制了测试用的高温高压伺服控制流变设备。袁龙蔚近年研究流变断裂学取得新进展，并将应用于研究岩体流变。

在研究地下工程围岩的稳定分析、破坏过程及其与支护结构的相互作用时，岩体的流变性是必须考虑的因素。离开流变观点，衬砌支护毫无意义。

此外，它对高边坡、坝基等岩体工程的理论和实践也极为重要，因此，岩体流变学已成为围岩稳定分析和支护结构设置及岩体工程的理论基础。

试验工作是了解岩石和岩体流变属性的主要手段，在试验工作基础上，通常采用两种方法来分析研究岩体流变问题，即模型法与继效法，岩体流变学研究的根本目的，是建立岩石(岩体)的本构方程，确定岩石流变参数，并以此来定性及定量的描述岩石变形与应力及时间的关系，进而解决地下工程实际问题。

人们根据对岩石的蠕变试验，松驰试验的结果，结合工程现场的调查、分析确定岩体的流变力学模型，建立岩体的本构关系，作为岩体流变性研究的基础。

关于岩体的流变模型，到目前为止，各国研究者采用的已有10多种，分为三大类，即弹性模型类、粘性模型类及塑滑性模型类。不同研究者，对不同地区不同类型的岩石，根据室内外岩石或岩体流变试验或观测推断，采用不同流变模型来代表各种岩体。通过流变模型的正确选择，推导本构关系，在变形不大的条件下，弹性力学中的平衡方程及几何方程仍可应用，只需用流变本构方程代替弹性力学中的广义虎克定律，可以证明，通过拉普拉斯变换，任何弹性力学可以求解的岩石力学问题，线性流变学也完全可以求解。

因为粘弹性体方程通过拉普拉斯变换，适当选取当量弹性常数后，就成了在相应面力和体力作用下与原粘弹性体有相同几何形状的弹性体问题，由弹性体解答经代换可得粘弹性体的拉普拉斯变换的解答，求其逆拉氏变换，而得粘弹性作解答。此法是E．H．Lee(1955)首先提出的，后来被称为“粘弹对应性原理”。

但此法在求逆拉氏变换时，常遇数学上困难，需采用技巧性方法巧妙处理。

在求解过程中还需确定诸流变参数，其数目等于流变模型的元件数。它们可通过实测求得，也可通过试验结合流变模型计算得到。

理论上，凡弹性力学可以求解的岩体力学问题，岩体的线性流变问题都可通过拉普拉斯变换求解。

但对地下结构的许多实际问题，还难以藉这类解析解求算结果，至于非线性流变问题，除一些极简单问题外，更难以用解析方法求得封闭解，往往需求助于数值解，电子计算机的发展提供了实施各种数值分析的条件。

岩体流变学的数值方法近年来得到很大的发展，各种方法应运而生，其中应用最为普遍的首推有限单元法，其次边界元法以及以这两种相耦合或派生出来的其他方法。

经过30年的努力，有限元法已成为一种相当完善和成熟的数值方法，能用以求解包括粘塑性及非牛顿体在内的所有时效非线性问题，并已在大型岩体工程结构物的设计施工中得到广泛采用。岩体流变问题的有限元解法，一般采用时间步长－荷载增量初应变法迭代计算，即将粘性应变看成初应变，每一时步迭加上相应的初应变增量，对于线性流变问题，只要连续不断地解线性弹性方程直至材料变形趋于稳定为止。

现以山岩洞室开控问题为例，说明解法的思路与步骤。

设总应变｛ε｝，包括弹性应变｛ε_e｝和粘性应变｛ε_v｝，即

｛ε｝=｛ε_e｝+｛ε_v｝ (1)

设单元e内存在初应变｛ε_v｝；弹性应｛ε_e｝与应力｛σ｝成线性关系，即物理方程为

｛σ｝=［D］｛ε_e｝=［D］(｛ε｝－｛ε_v｝ (2)

几何方程为

｛ε｝=［B］｛δ｝^e (3)

式中，D、B分别为弹性矩阵、几何矩阵。

由平衡方程，并结合式(2)，(3)，可得单元节点力

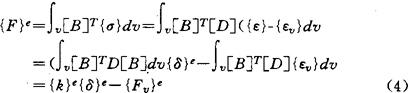
因此，可把粘性应变｛ε_v｝当作初应变，｛F_v｝^e表示粘性初应变产生的单元节点附加荷载，即

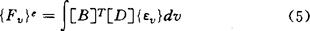
单元刚度矩阵

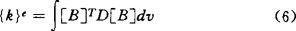
故总体平衡方程为

［k］｛δ｝=｛F｝+｛F_v｝ (7)

总刚度矩阵

［k］=∑｛k｝^e (8)

粘性应变所产生的总的附加结点荷载

｛F_v｝=∑｛F_v｝^e (9)

设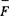｛｝为节点荷载，对于山岩洞室开挖问题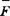，｛｝相当于作用于开挖边界节点释放荷载。此时，由(2)式得到的即由开挖引起的释放应力场｛σ_r｝，总的应力场｛σ｝为释放应力场｛σ_r｝与初始地应力场｛σ_d｝的迭加。

开挖问题，平衡方程(7)式的求解过程：

1．开挖阶段：在成洞之初，粘性应变尚未发展，即t=0时，｛ε_v｝=0，｛F_v｝=0。故由平衡方程(7)式，可求得成洞瞬时的位移场｛δ｝。

进而可得成洞瞬时总应力场｛σ｝。

2．粘弹性或粘塑性阶段：在任一时步t_i，都需把每个单元的总应力｛σ｝_i化为主应力［σ₁σ₂σ₃］^T，并按下式计算主应力平均值σ_m和等效应力：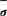

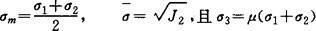
式中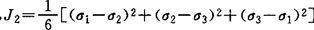， (10)

利用屈服函数，判断单元是否进入塑性状态。

当采用莫尔－库仑准则时，由下式计算屈服函数

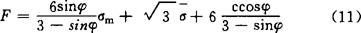
若F＜0，则该单元属粘弹性阶段，否则为粘塑性阶段，各单元逐一判断。

粘弹性阶段时，粘性应变可根据所采用的流变模型计算得到，例如对于kelvin模型。

在t_i－1到t_i(Δt=t_i－t_i－1)时刻对(12)式积分，并认为σ在t_i－1到t_i时刻内保持不变，于是有

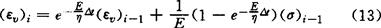
推广到多维应力状态，则为

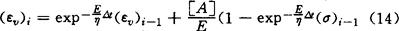
式中［A］为泊松比矩阵，对于平面应变问题为：

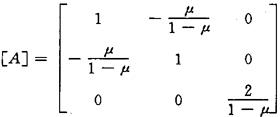
求得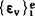，就可由(5)式求附加节点荷载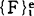，各单元都照此办理，并按(9)式，求总的粘性附加节点荷载｛F_v｝_i。

有了｛F_v｝_i，就可以由(7)式(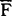｛｝已知)求位移场并由(2)、(3)式求｛ε｝_i｛σ｝_i。

每一时步重复以上步骤计算，直至应力或应变变化率逐步减小最后趋于零为止。

当经过若干时步计算后，设在t_j时刻，某一单元出现屈服函数F＞0，则该单元此时刻开始进入粘塑性阶段。

此时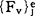仍可按(5)式求算，但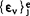要改为粘塑性应变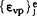，它可根据相应流变模型求得，共余类推。

对于非线性流变问题的有限元解法可类似地采用时步一初应变法描述，仍把粘性应变视为初应变，并由(5)求｛F_v｝^e。

但此时，由于应力应变关系是非线性的，因此，总体平衡方程是非线性的，总刚阵［k］不再是常刚阵，而与应力应变有关，因此，每一时步都需用求解非线性方程的方法求解总体平衡方程。

继有限元法之后，边界元法是求解复杂工程力学问题的又一种有力数值方法。

它是在边界积分方程(把线性偏微分方程的边值问题归化为等价的边界积分方程求解)基础上，借助有限单元的思路，把边界离散化，并采用相应插值函数，这就成了“边界元法”，它是Kizzc于1967年首先采用的。

一般的边界积分方程难有严密的解释解，但用数值方法求解时，只需把边界离散为边界单元，并在其节点之间插值，就可以把边界积分方程转变为线性代数方程组，由此解出各边界单元节点处的待定边界值，再利用边界值与域内函数值关系式，计算区域内任一点函数值。

对于粘塑性问题，可由平衡方程、几何方程和物理方程，演引得到三维粘塑性问题控制微分方程，对它取拉普拉斯变换，除去时间变量，而获得一个在变换空间的线性微分方程，就可用边界元法求解，再用数值逆变换法，可得原问题随时间变化的数值解。

。

【参考文献】：

1 Lee E H. Quart Appl Mth,1955,13

2 Nishihara M. Doshisha Engng Rev ,1958,8

3 Eienkiewicy O C. Int. J. Mech Sci, 1968,10

4 Vyalov S S. Rheological Fundamentals of Sail Mechanics, Elsevier Science Pullishers,1986

5 孙钧主编．岩石力学新进展．吉林：东北工学院出版社，1989

6 陈德坤．岩体的流变性对固定稳定性的影响．中国科技成果大辞典．1995，1110

(上海城市建设学院陈德坤教授撰)