例2 已知f(x)=1+logx3,g(x)=2logx2,试比较f(x)与g(x)的大小.
解 f(x)=logx3x,g(x)=2logx2=logx4.
∴f(x)—g(x)=logx3x—logx4=logx3/4x.
当0
当1 logx3/4x<0,有f(x) 当x=4/3时,3/4x=1, logx3/4x=0,有f(x)=g(x); 当x>4/3时,3/4x>1, logx3/4x>0,有f(x)>g(x); 综上可知,当0 当x=4/3时,f(x)=g(x); 1 例3 已知函数y=loga(2—ax)在[0,1]上是x的减函数,求a的取值范围. 解 ∵a>0且a≠1, ∴设μ=2—ax,则μ为减函数, 又∵y=logax在0 ∴y=logaμ为增函数, ∴a>1. ❶ 另一方面,当0≤x≤1时,2—ax>0恒成立, 即 ∴只需 由❶ ❷ 可知:1 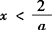 恒成立
恒成立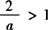 即a<2.❷
即a<2.❷
- 虞抟是什么意思
- 虞挥是什么意思
- 虞授是什么意思
- 虞搏是什么意思
- 虞放是什么意思
- 虞敏是什么意思
- 虞文伯是什么意思
- 虞文靖公全集文是什么意思
- 虞文靖公年谱是什么意思
- 虞文靖公诗集是什么意思
- 虞方简是什么意思
- 虞旗是什么意思
- 虞易简是什么意思
- 虞昭商頀是什么意思
- 虞晓冰是什么意思
- 虞景豫是什么意思
- 虞曰鎮是什么意思
- 虞曹是什么意思
- 虞曹郎是什么意思
- 虞曹郎中是什么意思
- 虞望是什么意思
- 虞朝宗是什么意思
- 虞术是什么意思
- 虞村是什么意思
- 虞杨范揭是什么意思
- 虞松退姜维是什么意思
- 虞某是什么意思
- 虞桥是什么意思
- 虞棘是什么意思
- 虞槃治妖巫安定民心是什么意思
- 虞歌诀别是什么意思
- 虞歌骓逝是什么意思
- 虞殡是什么意思
- 虞氏是什么意思
- 虞氏易义补注是什么意思
- 虞氏易事是什么意思
- 虞氏易候是什么意思
- 虞氏易消息图说是什么意思
- 虞氏易礼是什么意思
- 虞氏易言是什么意思
- 虞氏易象汇编是什么意思
- 虞氏易象考证是什么意思
- 虞氏春秋是什么意思
- 虞氏记是什么意思
- 虞永兴是什么意思
- 虞汜是什么意思
- 虞汲是什么意思
- 虞沅是什么意思
- 虞沅芍药八哥图轴是什么意思
- 虞泉是什么意思
- 虞泉州是什么意思
- 虞泉敛暝是什么意思
- 虞泉日沉是什么意思
- 虞洮是什么意思
- 虞洽卿是什么意思
- 虞涻卿是什么意思
- 虞淳熙是什么意思
- 虞淵是什么意思
- 虞清华是什么意思
- 虞渊是什么意思