自康托(G.Cantor)在1873年创立朴素集合论后,人们对数学的认识便进入一个新的境界。
但由于1901年罗素(B.Russell)在朴素集合论中发现了悖论,使人们认识到康托给集合下的定义是有缺陷的。为了消除悖论,便促成了策墨罗(E.Zermelo)和弗伦克尔(A.A.Fraenkel)为代表创立的ZF公理系统的诞生。
然而ZF公理系统是不完善的,象连续统假设这样深刻的问题已被证明在该系统内是不可判定的。这是哥德尔(K.Gödel)于1938年和柯恩(P.J.Cohen)于1963年工作的结果。
虽然也还有其它一些公理系统出现,但也未获得令人满意的结果,这就促使人们在某种意义上不得不“从头开始”。
由于给集合下定义会带来麻烦,因此集合被认为是不定义的概念。
它通常被描述成:“一些对象的全体”(以下简称“P”)或类似的说法。而具体解释这些对象时,又要求称作元素的对象要有“确定”、“互异”两个特性。
这与P已有了相当的差别,事实上仅由P所得到的集比我们现在通常所说的集要广泛得多。但也要注意,P中的“一些”是不能用“全部”来替换的。
既然集合是不定义的概念,如何较好地描述这个概念仍然是值得考虑的。即使是这样,集合论在早期的研究中亦产生一些相当重要的结果。
又因这些结果大都涉及到数学的“根基”,因而“数学基础”的研究也随之蓬勃开展起来。
那么,仅由P来讨论集合会得到一些什么结果呢?首先应提到的就是扎德(L.A.Zadeh)在1965年给出的F集。F集的问世,被认为是“确定性”这条限制的破缺,并由此拓宽了经典集合论研究的范围。
然而实际上,F集的重大意义是提示了非整集的存在。
由于P中并未说明元素不许重复,因此若去掉互异性的限制,我们就再次地扩大了集合的范围。因为相同的元素(比如5个3)确确实实可构成一个集合。
这实际上是将集合中每个不同的元素皆以一个数值λt——称为“位置值”来标明。将λt限定在[0,1]中讨论时,便构成F集理论。
λt仅取{0,1}中的值时即为经典集,即经典集中的元素被安排在实轴的0,1两个点上且与论域U有关。一般λt可在高斯平面上找到其对应点。当某集的λt仅取实数时,称某集为实集;当某集的λt取复数时,则称某集为复集。尤其是当集A中的元素ut位置值λt为自然数m时,即表明A中有m个同样的元素ut,而λt的值为-m时,即表明若在A中加入m个ut后,A中ut的“个数”将变为零。
从上面的论述中可以看到:人们对于“两个特性”的认识,是经过认可-破缺-高一层次的认可的曲折过程的。
为了论述方便,下面我们简略地给出复集的定义、运算和一些有关方面的内容。
定义1 所谓给定了论域U={ut|t∈T}上的一个复集A,是指对于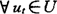 都指定了一个复数λ(ut)∈C,叫做ut对A的位置值。映射λ(·):U→C,ut→λ(ut)叫做A的位置函数,其中C为复数集。
都指定了一个复数λ(ut)∈C,叫做ut对A的位置值。映射λ(·):U→C,ut→λ(ut)叫做A的位置函数,其中C为复数集。
特别是
λ(·)∶U→R,则称A为实集;
λ(·)∶U→[0,1],则称A为F集;
λ(·)∶U→{0,1},则称A为经典集;
λ(·)∶U→{0},则称A为零集,记作OU。
这里0U是指对U而言的零集,一般若U≠V,则OU≠Ov,当考虑某问题不会引起误解时可省去下标。
至少有一个ut,使λ(·):ut→λ(ut)且λ(ut)∈C-R,则称A为虚集。
由于复集由其论域和位置函数所刻画,所以复集的表法有下面几种:
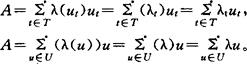
可视不同场合而选用最简记法,并且当λ(ut)=1时可省略λ(ut)。
为简明起见,常使用第一行中的记法。其中“∑”表A的所有元素连同位置函数的一个总括。特别指标集T为可数集时,
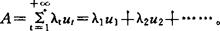
其中“+”即表A的元素连同位置值的一个列举。
在研究某具体问题时,对于给定的T0,若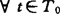 ,有λt=1,则
,有λt=1,则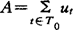 即可作为该问题的论域U0。
即可作为该问题的论域U0。
因此若T0≠T1,常有U0≠U1,这在复集问题的讨论中须特别注意。
复集A中的元素可通过其位置值在高斯平面上表示出来。U上全体复集所构成的集类记作C(U),类似有R(U)等等。
定义2 若n元函数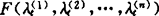 有意义,并设A(j)
有意义,并设A(j)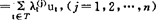 ,则
,则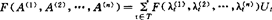 ,尤其当n=2时,有
,尤其当n=2时,有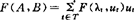 。
。
其中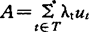 ,
,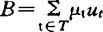 。
。
由定义2不难证明:
定理1 若f(λt)有意义,则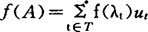 。
。
推论 若f(λt)=0,则f(A)=0。
由定义2及定理1,可得一系列运算法则。
这里从略,在这里再一次强调论域U的重要性。作为一个具体的例子,可以在复集中证明,欧拉公式亦成立:
cosA+isinA=eiA。
定义3 设函数F的变元为集,则称F为集函数。当X(j)∈C(U)时,称F(X(1),X(2),…,X(n))=0为n元复集函数(j=1,2,…,n)。
当某集为变元时,可称该集为变量集,否则称常量集。特别,当X∈C(U)和X∈R(U)时,分别称Y=f(X)为一元复集显函数和一元实集显函数。显然,一个集函数由对应关系和论域所确定。
定义4 含有未知集的等式叫做集方程,简称方程。
解出未知集的过程叫解集方程。若某集替换方程中的未知集后可使方程成为恒等式,则该集就称为集方程的集解,简称为解。
解方程的方法与解代数方程或微分方程(若集方程中含有关于未知集的微分运算的话)的解法类似,所不同的只是解方程时要先求出论域U。特别有下面的定理2:
定理2 若一元n次集方程有解,则解的个数为nm,其中m=cardU。
对于实集,可以考虑包含关系。用包含符号: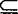 (含于)
(含于)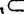 (真含于)等联结的式子称实集包含式,关于实集包含式有下面的定理3:
(真含于)等联结的式子称实集包含式,关于实集包含式有下面的定理3:
定理3 设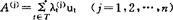 ,则f(A1,A2,…,An
,则f(A1,A2,…,An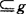 (A1,A2,…,An)的充要条件是f(λ1,λ2,…,λn)≤g(λ1,λ2,…,λn)。由该定理可以获得一批有价值的实集包含式。
(A1,A2,…,An)的充要条件是f(λ1,λ2,…,λn)≤g(λ1,λ2,…,λn)。由该定理可以获得一批有价值的实集包含式。
定义5 设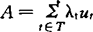 ,(λt∈C),若
,(λt∈C),若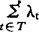 有意义,则称
有意义,则称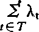 为A的复势并简称为势,仍记作cardA。
为A的复势并简称为势,仍记作cardA。
显然该定义包含了实集势的定义。
由定理1知|A|为实集,因而有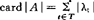 (这里设等式右端有意义),我们称card|A|为复集A的模势。
(这里设等式右端有意义),我们称card|A|为复集A的模势。
另外在应用中有时还要考虑复势模: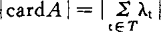 。复势、模势和复势模在复集理论中各有不同的作用。
。复势、模势和复势模在复集理论中各有不同的作用。
以上只论述了实集和复集的几个基本方面,实集和复集涉及的范围比较广泛,本文不可能都一一列举到。由于该理论的研究时间不长,预计在今后若干年内将有较大的进展,特别是其逻辑基础与应用将成为研究的热点。
。【参考文献】:1 Hausdorff F著.集论.张义良,颜家驹译.北京:科学出版社,1960
2 Andrzej Mostowski著.数学基础研究30年.郭世铭等译.武汉:华中工学院出版社,1983
3 Zadeh L A著.模糊集合、语言变量及模糊逻辑.陈国权译.北京:科学出版社,1982
4 朱梧槚编著.几何基础与数学基础.沈阳:辽宁教育出版社,1987
5 孙桂秋.湖南科技大学学报,1987,2∶17~28
6 张锦文,王雪生.连续系统假设.沈阳:辽宁教育出版社,1988
(湖南中医学院分院孙桂秋撰)
- 金阵是什么意思
- 金阶是什么意思
- 金阿庆是什么意思
- 金阿林是什么意思
- 金陀僧是什么意思
- 金陀别馆是什么意思
- 金陀粹编是什么意思
- 金陀粹编、续编是什么意思
- 金陀续编是什么意思
- 金附是什么意思
- 金附国是什么意思
- 金附州都督府是什么意思
- 金陈是什么意思
- 金降落伞是什么意思
- 金降落伞战术是什么意思
- 金降落伞计划是什么意思
- 金院本是什么意思
- 金陵是什么意思
- 金陵三俊是什么意思
- 金陵三首是什么意思
- 金陵三首 (唐)李白是什么意思
- 金陵丛书是什么意思
- 金陵丛刻是什么意思
- 金陵东园是什么意思
- 金陵之王气是什么意思
- 金陵二主是什么意思
- 金陵五题是什么意思
- 金陵五题·石头城是什么意思
- 金陵五题(五首选三)是什么意思
- 金陵五题其一石头城2是什么意思
- 金陵八大家是什么意思
- 金陵八家是什么意思
- 金陵六院市语是什么意思
- 金陵刻经处是什么意思
- 金陵十二钗是什么意思
- 金陵十二钗后传是什么意思
- 金陵十二钗图册判词是什么意思
- 金陵十二钗正册判词(警幻仙姑) 林黛玉、薛宝钗是什么意思
- 金陵协和神学院是什么意思
- 金陵协和神学院(南京)是什么意思
- 金陵历代建置表是什么意思
- 金陵历史建置表是什么意思
- 金陵古今图考是什么意思
- 金陵古金石考是什么意思
- 金陵名贤帖是什么意思
- 金陵后观棋(其五) - 清·钱谦益是什么意思
- 金陵图是什么意思
- 金陵城是什么意思
- 金陵城西楼月下吟是什么意思
- 金陵城西楼月下吟 - 唐·李白是什么意思
- 金陵夜寂凉风发,独上高楼望吴越。 白云映水摇空城,白露垂珠滴秋月。是什么意思
- 金陵大学是什么意思
- 金陵大学图书馆方志目是什么意思
- 金陵太极是什么意思
- 金陵太极拳是什么意思
- 金陵女子文理学院是什么意思
- 金陵子弟来相送,欲行不行各尽觞。是什么意思
- 金陵 - 宋·苏泂是什么意思
- 金陵官书局是什么意思
- 金陵寺镇是什么意思