1.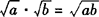 (a≥0,b≥0).
(a≥0,b≥0).
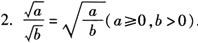
注意 1.公式的逆变形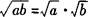 (a≥0,b≥0).
(a≥0,b≥0).
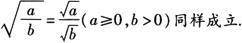
2.公式中的a、b可以是单项式还可以是多项式,但要保证被开方式大于等于零.
例1 一个实数与它的相反数的倒数的和是零,这个实数是( ).
A.0 B.1
C.-1 D.±1
答 D.
[解析] 0没有倒数.
例2 绝对值小于3的所有实数的积为( ).
A.6 B.12
C.0 D.-6
答 C.
[解析] 0的绝对值小于3;
0乘以任何数都得0.
例3 负数a减去它的相反数差是( )
A.2a B.0
C.-2a D.a-1/a

[解析] 有理数范围内的运算法则及公式在实数范围内仍适用.

请你将猜想到的规律用含正整数n的代数式表示出来:__.
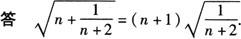
[解析] 每个等式左边被开方数中第一个加数为连续的自然数,第二个加数是比第一个加数大2的倒数,每个等式右边被开方数恰好为左边被开方数中的第二个加数,前面的系数比其被开方数中的第一个加数大1,所以猜想规律为
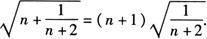
- 愣住是什么意思
- 愣倯是什么意思
- 愣儿是什么意思
- 愣充是什么意思
- 愣充近枝儿是什么意思
- 愣冲冲是什么意思
- 愣可是什么意思
- 愣呆呆是什么意思
- 愣呵呵是什么意思
- 愣啦巴唧是什么意思
- 愣头是什么意思
- 愣头儿葱是什么意思
- 愣头儿青是什么意思
- 愣头巴脑是什么意思
- 愣头愣脑是什么意思
- 愣头磕脑是什么意思
- 愣头福是什么意思
- 愣头葱是什么意思
- 愣头青是什么意思
- 愣实是什么意思
- 愣小子是什么意思
- 愣巴是什么意思
- 愣巴巴是什么意思
- 愣怔是什么意思
- 愣怔怔是什么意思
- 愣愣儿是什么意思
- 愣愣实实是什么意思
- 愣愣怔怔是什么意思
- 愣愣柯柯是什么意思
- 愣愣磕磕是什么意思
- 愣愣𪫧𪫧是什么意思
- 愣愣𪫾𪫾是什么意思
- 愣扯是什么意思
- 愣捶是什么意思
- 愣是是什么意思
- 愣梅是什么意思
- 愣棒是什么意思
- 愣沉是什么意思
- 愣渴鸪是什么意思
- 愣爹是什么意思
- 愣登是什么意思
- 愣登登是什么意思
- 愣的呵是什么意思
- 愣的怕硬的,硬的怕不要命的是什么意思
- 愣目愣眼是什么意思
- 愣眉愣眼是什么意思
- 愣眼儿巴唧是什么意思
- 愣眼儿巴睁是什么意思
- 愣眼儿瓜哒是什么意思
- 愣眼巴睁是什么意思
- 愣瞌瞌是什么意思
- 愣瞪是什么意思
- 愣磕磕是什么意思
- 愣神是什么意思
- 愣神儿是什么意思
- 愣种是什么意思
- 愣葱是什么意思
- 愣视是什么意思
- 愣话是什么意思
- 愣里愣怔是什么意思