绕定点o转动的刚体的动力学方程就是动量矩定理。
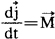
在写分量式时,为方便计,常选取固著在刚体上和刚体一起转动的动坐标系(o-xyz),并常选用o点上的惯量主轴为x、y及z轴,此时有欧勒动力学方程
I1ωx-(I2-I3)ωYωz=Mx
I2ωy-(I3-I1)ωzωx=MY
I2ωt-(I1-I2)ωxωY=Mz
式中I1、I2及I3为绕惯量主轴x,y及轴的转动惯量,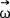 表示角速度,顶上带撇表示对t的微商,
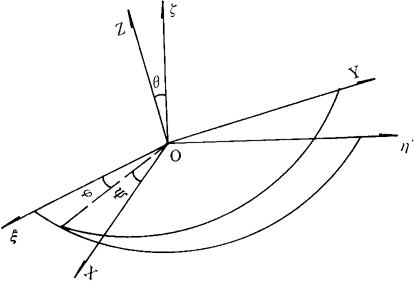
表示角速度,顶上带撇表示对t的微商,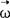 的三个分量ωX、ωY及ωz可分别写成(常称欧勒运动学方程)式中三个欧勒角(进动角φ,自转角ψ及章动角θ)的定义可参见右图,图中
的三个分量ωX、ωY及ωz可分别写成(常称欧勒运动学方程)式中三个欧勒角(进动角φ,自转角ψ及章动角θ)的定义可参见右图,图中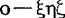 及o xyz分别为固定坐标系及动坐标系。
及o xyz分别为固定坐标系及动坐标系。
ωx=φsinθsinψ+θcosψ
ωy=φsinθcosψ-θsinψ
ωz=φcosθ+ψ
从理论上讲,求定点转动的刚体的运动归结为从欧勒动力学方程(结合欧勒运动学方程)解出θ、φ及ψ随时间t的函数关系,实际上,除少数典型例子外,这种计算往往是很繁难的。
- 丑女赋是什么意思
- 丑奴是什么意思
- 丑奴儿是什么意思
- 丑奴儿 书博山道中壁(辛弃疾 )是什么意思
- 丑奴儿令是什么意思
- 丑奴儿令(冯夷剪碎澄溪练)是什么意思
- 丑奴儿(夜来酒醒清无梦)是什么意思
- 丑奴儿 - 宋·辛弃疾是什么意思
- 丑奴儿慢是什么意思
- 丑奴儿慢 黄景仁是什么意思
- 丑奴儿 木樨是什么意思
- 丑奴儿近是什么意思
- 丑奴儿近 博山道中,效李易安体(辛弃疾)是什么意思
- 丑妇是什么意思
- 丑妇免不得见公姑是什么意思
- 丑妇免不得见公婆是什么意思
- 丑妇家中宝是什么意思
- 丑妇家中宝。是什么意思
- 丑妇家中宝,可喜惹烦恼是什么意思
- 丑妇效颦是什么意思
- 丑妇终须见姑嫜是什么意思
- 丑妇角色是什么意思
- 丑妇赋是什么意思
- 丑妈妈是什么意思
- 丑妻是什么意思
- 丑妻家中宝是什么意思
- 丑姑姑是什么意思
- 丑姑娘是什么意思
- 丑姹是什么意思
- 丑姿八怪是什么意思
- 丑娸是什么意思
- 丑婆娘好搽粉是什么意思
- 丑婆子是什么意思
- 丑媟是什么意思
- 丑媳妇不说自己难看,埋怨镜子上锈是什么意思
- 丑媳妇也得见公婆是什么意思
- 丑媳妇免不得要见公婆是什么意思
- 丑媳妇免不得见公婆是什么意思
- 丑媳妇少不得见公婆。是什么意思
- 丑媳妇怕不得见舅姑是什么意思
- 丑媳妇怕见公婆是什么意思
- 丑媳妇怕见公婆面是什么意思
- 丑媳妇怕见婆家人是什么意思
- 丑媳妇总得见公婆是什么意思
- 丑媳妇总得见公婆面是什么意思
- 丑媳妇总要见翁姑是什么意思
- 丑媳妇见公婆是什么意思
- 丑媳妇见公婆——总有一次难看是什么意思
- 丑子是什么意思
- 丑子冈是什么意思
- 丑官是什么意思
- 丑官儿是什么意思
- 丑宝是什么意思
- 丑宝丸是什么意思
- 丑容是什么意思
- 丑寳是什么意思
- 丑寺村是什么意思
- 丑小鸭是什么意思
- 丑差是什么意思
- 丑巴怪是什么意思