大筛法

---

近代解析数论的重要工具。

大筛法首先由苏联数学家列尼克为研究模p的正的最小二次非剩余而提出的。瑞尼进一步推广和发展了大筛法，并将它成功地应用于哥特巴赫猜想的研究之中，首先得到了(HC)这一著名结果。后来，朋比尼等人又进一步完善和简化了大筛法的形式和证明，使之更成功地应用于解析数论，并改进了一系列经典解析数论问题的结果。

设δ是任一大于零的正数，若实数列X_i(0≤i≤k)满足条件：x₀＜x₁＜…＜xk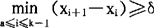，，则称数列x_i(0≤i≤k)是一个δ佳位组。若a_n，MH≤n≤M+N为任意复数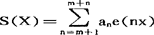，。再设x₁，0≤x_i≤1，0≤i≤k为一δ佳位组，大筛法就是研究和式的上界估计。

显然，大筛法应该是筛法的一种，它的名称也应相对于小筛法(即通常的筛法)而言的。

设A是一个由有限多个整数所组成之集，Z＞2，P是一个由有限个不同素数P(P≤X)所组成的集合。

再设对每一个素数p∈P，给定模p的λ(p)个不同的剩余类：h_p，1，h_p，2，…，h_ρ，λ(p)。在集合A中筛去所有满足下述条件的元素n：n，1≤j≤λ(p)，p∈p，将筛剩下来的A的子集记为N，并设其元素个数为Z，这就是筛法。筛法所研究的主要问题就是估计Z的上界和下界，按照所有的λ(P)是“大”还是“小”(在某种平均意义上)，就称对应的筛法为大筛法或小筛法。例如，取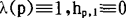，这就是小筛法。

列尼克首先考虑了这样的问题：设集合A是由整数MH，M+2，…，M+N组成，取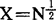而P是由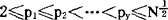这不同的y个素数组成。设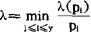且满足0＜λ＜1，列尼克证明了对Z有估计：Z《N／λ²y成立。

由于这里的λ(p_i)≥λp_i，所以是“大”的，因而列尼克把他的方法称为大筛法。