多因子模型

---

多因子模型是关于资产定价的模型。

与资本资产定价模型和单指数模型不同，多因子模型认为证券价格并不仅仅取决于证券的风险，还取决于其他一些因素，如，投资者未来预期收入、未来消费品的相对价格及未来的投资机会等。

多因子模型的理论背景是Ross基于套利原理创立的套利定价理论(APT)和Merton基于均衡原理创立的跨时期资本资产定价模型(ICAPM)。套利定价理论假定市场是竞争的和无摩擦的，资产的收益产生过程如下：

R_i=a_i+b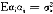f+ε_i

E[ε_i∶f]=0

E[ε_iε_i]=σ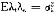≤σ²＜∞

R=a+Bf+ε

E[ε_i∶f]=0

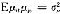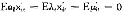E[ε]=σ≤σ²＜∞

其中，R_i是资产i的收益，a_i是截距，b_i是K×1维的资产i对于因素的敏感度向量，f是K×1维的因素刻画向量，ε_i是扰动项。对于N种资产，在方程组中，R是一个N×1向量，R=[R₁，R₂…，R_N]′，a是一个N×1向量，a=[a_i]′，B是一个N×K矩阵，B=[b₁，b₂，…，b_N]′，ε是一个N×1向量，ε=[ε_i]′，在这种情况下，套利的消失意味著

μ≈τλ₀+Bλ_K

其中μ是一个N×1期望收益向量，λ₀是模型的零β参数，相当于无风险资产，λ_k是N×1风险溢价向量。