多元正态分布

---

随机向量的一种分布。

一元正态分布的推广。若p维随机向量Y′=［Y₁，Y₂，…，Y_p］的(联合)密度函数是f(y)=(2π)^－p／2·｜∑｜－^1／2·exp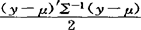｛－｝，(y∈R_p)，这里y′=(y₁，y₂，…，y_p)，μ=E(Y)=(μ₁，μ₂，…，μ_p)′∈E_p(E_p为p维欧氏空间)，∑=V_ar(Y)=［σ_ij］_p×p，是p阶正定对称矩阵，则称Y服从p维(元)正态分布，记为Y～N_p(μ，∑)。当p=2时，得到二元正态分布。

若V_ar(Y)=σ²I=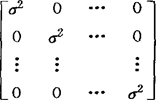，则f(y)=(2π)^－p／2·｜σ²I｜^－1／2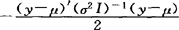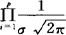·exp｛｝=·exp｛｝。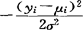

此时Y的密度函数等于其各分量Y_i(i=1，2，…，p)的密度函数之乘积，而Y_i～N(μ_i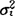，)，即Y的各分量是彼此独立的正态分布，常简记为Y～N_p(μ，σ²I)。多元正态分布理论是多元统计分析的重要理论基础。