复合函数的导数

---

法则4 复合函数对自变量的导数，等于已知函数对中间变量的导数，乘以中间变量对自变量的导数，即y′_x=y′u·u′_x．

例 下列函数是由一些简单的函数复合而成的，写出它们的复合过程，并求出它们关于x的导数．

(1)y=(x²+2x)³；

(2)y=e^5+4x2；

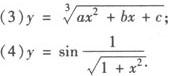
解 中间变量的设置，以基本初等函数为最小单位，直接利用基本公式表求导．

(1)y=u³，u=x²+2x，y′=3u²·u′

=3(x²+2x)²(x²+2x)′

=3(x²+2x)²(2x+2)．

(2)y=e^u，u=5+4x²，

y′=e^u·u′=e^5+4x2·8x．