基数

---

对集合进行研究的一个重要方面是研究集合中元素的多少，集合的基数便是用来衡量集合中元素的多少的。

为了比较两个集合的元素的多少，我们还需引进集合等价的概念。

如果存在从集合A到集合B上的1－1函数，则称A与B是等价的，或称A与B等势。显然，我们有：(1)A与A等价；(2)如果A与B等价，则B与A等价；(3)如果A与B等价并且B与C等价，则A与C等价。因此，我们可以按此等价关系将集合分成一些两两互不相交的类，使每个集合都属于某个类，并且集合A与B在同一类中当且仅当A与B等价。

上述分类中的每一类都有自己的一种特征性质，根据这个特征性质，决定一个集合是否属于这个类。我们把集合A所在的类的特征性质称为A的基数，并用｜A|表示它。

上面关于集合基数的描述并不是严格的数学定义，但这并不影响理论的发展。事实上，我们只要求基数满足下面这个式子便行了：

｜A|=｜B|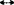存在从A到B上的1－1函数。

我们说A的基数小于或等于B的基数，如果A与B的某个子集的基数相等，用符号表示为|A|≤｜B｜。如果｜A|≤|B|并且｜A|≠｜B｜，则称A的基数小于B的基数，记为|A|＜|B｜。

基数的许多性质与我们熟悉的有穷集的元素的个数的性质相同，基本的有：

(1)｜A｜=|A｜

(2)｜A≤｜B｜∧｜B｜≤｜A｜→|A｜=｜B｜

(3)|A｜≤｜B|∧B｜≤|C｜→|A｜≤|C｜

(4)

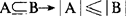
基数也有些与有穷集的元素的个数性质不同的性质。比如，一个集合的基数可以与它的一个真子集的基数相等。

我们用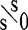(阿列夫零)表示自然数集的基数，用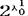表示实数集的基数。康托证明了下面的不等式

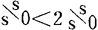
康托自己一直没有找到基数大于s／s₀并且小于2^s／s0的集合。他提出猜想：这样的集合是不存在的。这便是著名的连续统假设。

后来，人们证明了这个假设与通常的集论公理是独立的。

康托还定义了基数的算术运算它是自然数的算术运算的推广。