式子y=f(x)表示y是自变量x的函数,设它的定义域为A,值域为C,我们从式子y=f(x)中解出x,得到式子x=φ(y).如果y在C中的任何一个值,通过式子x=φ(y),x在A中有惟一的值和它对应,那么式子x=φ(y)就表示x是自变量y的函数.这样的函数x=φ(y),叫做函数y=f(x)的反函数,记作x=f—1(y).
1.反函数存在的条件
若函数y=f(x)的定义域为A,值域为C,且函数所确定的映射是A到C的一一映射,则该函数存在反函数.
2.原函数与反函数的关系
(1)函数y=f(x)的定义域、值域分别是反函数y=f—1(x)的值域、定义域.而反函数的定义域必须通过求原函数的值域得到.
(2)一般地,函数y=f(x)的图象和它的反函数y=f—1(x)的图象关于直线y=x对称.
(3)图象间的关系:y=f(x)与x=f—1(y)是同一图象,而y=f(x)与y=f—1(x)图象关于直线y=x对称.
3.求一个函数f(x)(x∈D)的反函数分三个步骤:
(1)由y=f(x)解出x=f—1(y);
(2)x、y位置互换,得到y=f—1(x);
(3)标明反函数定义域(即原函数值域).
4.两个有用的结论
(1)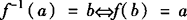 .
.
(2)f[f—1(x)]=x,x∈f(x)的值域,
f—1[f(x)]=x,x∈f(x)的定义域.
5.函数与反函数的关系(如下表)
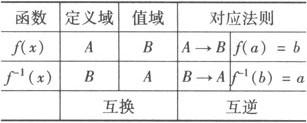
例1 求下列函数的反函数:
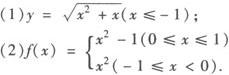
分析 按求反函数的方法分步求解.
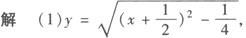
易知在x≤—1时,函数是递减函数,存在反函数,对原式两端平方,得y2=x2+x,
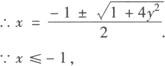
∴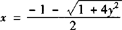 且原函数的值域为{y|y≥0}.
且原函数的值域为{y|y≥0}.
故所求的反函数为
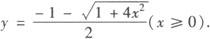
(2)当0≤x≤1时,—1≤x2—1≤0,
即—1≤y≤0.
由y=x2—1(0≤x≤1)得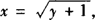 ,
,
∴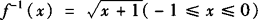 .
.
当—1≤x<0时,0 由y=x2(—1≤x<0)得 ∴ 综上所述 例2 若点(1,2)既在函数f(x)= 分析 利用互为反函数的两个函数图象之间的关系. 评析 由于互为反函数的函数图象关于直线y=x对称,因而点(1,2)在反函数f—1(x)的图象上时,其关于直线y=x的对称点(2,1)必在原函数的图象上. 例3 已知 解 ∵y=g(x)的图象与y=f—1(x+1)的图象关于直线y=x对称, ∴y=g(x)与y=f—1(x+1)互为反函数.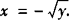 .
.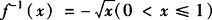 .
.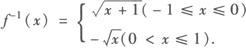
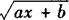 的图象上,又在其反函数f—1(x)的图象上,试确定f(x)的解析式.
的图象上,又在其反函数f—1(x)的图象上,试确定f(x)的解析式.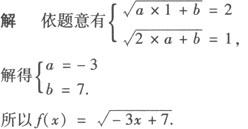
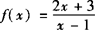 ,函数y=g(x)的图象与f—1(x+1)的图象关于直线y=x对称,求g(11)的值.
,函数y=g(x)的图象与f—1(x+1)的图象关于直线y=x对称,求g(11)的值.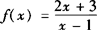 的反函数为f—1(x)=
的反函数为f—1(x)=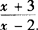 .
.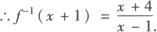
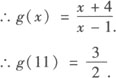
- 蘸水片是什么意思
- 蘸水笔是什么意思
- 蘸水钢笔是什么意思
- 蘸水钢笔——没有胆是什么意思
- 蘸油是什么意思
- 蘸涝是什么意思
- 蘸淊是什么意思
- 蘸火是什么意思
- 蘸甲是什么意思
- 蘸白糖啃鸭梨是什么意思
- 蘸的是什么意思
- 蘸盐醋是什么意思
- 蘸着稀饭吃扁食——越吃越糊涂是什么意思
- 蘸秧是什么意思
- 蘸秧根是什么意思
- 蘸立是什么意思
- 蘸笔是什么意思
- 蘸老是什么意思
- 蘸转来是什么意思
- 蘸酒是什么意思
- 蘸酱菜是什么意思
- 蘸釉是什么意思
- 蘸钢是什么意思
- 蘸钢子是什么意思
- 蘸闪是什么意思
- 蘸饵是什么意思
- 蘹是什么意思
- 蘹葇是什么意思
- 蘹香是什么意思
- 蘹香虫是什么意思
- 蘹香蟲是什么意思
- 蘺是什么意思
- 蘻是什么意思
- 蘼是什么意思
- 蘼儿是什么意思
- 蘼芜是什么意思
- 蘼芜君是什么意思
- 蘼芜媚香是什么意思
- 蘼芜山樵是什么意思
- 蘼芜本是什么意思
- 蘼芜花是什么意思
- 蘼蕪是什么意思
- 蘼豆是什么意思
- 蘽是什么意思
- 蘽芜是什么意思
- 蘽蕪是什么意思
- 蘾是什么意思
- 蘿是什么意思
- 蘿摩是什么意思
- 蘿蒿是什么意思
- 蘿蔔是什么意思
- 蘿蔔子是什么意思
- 蘿蔔菜是什么意思
- 蘿藦是什么意思
- 蘿蘼是什么意思
- 蘿軒變古箋譜是什么意思
- 虀是什么意思
- 虀料是什么意思
- 虀盐是什么意思
- 虀糟是什么意思