动态对策

---

是与同步对策相对的概念，它意味著局中人按一定顺序相继作出若干步决策。

动态对策理论通常依赖于以下基本假设：

(1)每个局中人了解每一结局的后果，且确信其对手也了解这一点。

(2)每个局中人能完全记住自己及对手已作出的所有策略选择。

对于动态对策通常考虑两种均衡概念：子对策精练纳什均衡与贝叶斯均衡。前者见"子对策精练纳什均衡"条目；后者简要解释如下。

设对一展开型对策的每个决策结点x，指定了概率μ(x)，使得对每个信息集H，有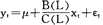μ(x)=1。对于信息集H、在H行动的局中人i及某个混合策略组σ=(σ_i，σ_－i)，若对i的任何其他混合策略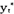_i，i在策略组(σ_i，σ_－i)下从H开始的期望收益不小于在(σ_i，σ_－i)下从H开始的期望收益，即：

E[u_i|H，μ，σ_i，σ_－i]≥E[u_i|H，μ，σ_i，σ_－i]

则说σ对H是序列合理的。

若σ对所有信息集H是序列合理的，且当P_rob(H|σ)＞0时，对任何x∈H有：

P_rob(x|σ)=μ(x)P_rob(H|σ)

则称σ为弱完全贝叶斯均衡，简称为WPBE。WPBE必为纳什均衡，反之则未必。