加权平均法有加权算术平均法、加权几何平均法等等,但一般是指加权算术平均法。
给定一组数据,当求它们的平均数时,常由于每个数据的重要性不完全相同,使得采用算术平均数作为该组数据的平均数并非一个最理想的办法。其最佳平均数应是把每个数据的重要性在计算平均数时考虑进去。具体方法是,把每一个数据的重要性估计一个称为“权数”的数值来代表,然后求每个数据与对应的权数之积的和,再把此和除以各个权数之和。这种计算平均数的方法与程序称为加权平均法,所得的平均数称为加权平均数。
设x1,x2,……,xn为给定的n个数据,w1,w2,……,wn为已知的对应权数。根据上述加权平均数的定义,加权平均数可用下式求得:
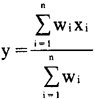
可简写为:
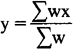
当给出的不是一组数据,而是连续变化的函数时,同样可求其加权平均数,只是给定的权数也必需是一个函数。设给定的连续数值为函数f(x),给定的权数为函数w(x),则求(a,b)区间内加权平均数的公式为:
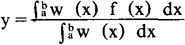
- 套间是什么意思
- 套鞋是什么意思
- 套餐是什么意思
- 套马是什么意思
- 套马杆是什么意思
- 奘是什么意思
- 奚是什么意思
- 奚仲是什么意思
- 奚落是什么意思
- 奠是什么意思
- 奠基是什么意思
- 奠基人是什么意思
- 奠基石是什么意思
- 奠定是什么意思
- 奠祭是什么意思
- 奠边府是什么意思
- 奠都是什么意思
- 奠酒是什么意思
- 奡是什么意思
- 奢是什么意思
- 奢丽是什么意思
- 奢侈是什么意思
- 奢侈品是什么意思
- 奢华是什么意思
- 奢念是什么意思
- 奢想是什么意思
- 奢望是什么意思
- 奢求是什么意思
- 奢糜是什么意思
- 奢谈是什么意思
- 奢靡是什么意思
- 奤是什么意思
- 奥是什么意思
- 奥丁是什么意思
- 奥义是什么意思
- 奥克兰是什么意思
- 奥克斯是什么意思
- 奥兰是什么意思
- 奥兰多是什么意思
- 奥利弗是什么意思
- 奥博是什么意思
- 奥博特是什么意思
- 奥古是什么意思
- 奥哈拉是什么意思
- 奥地利是什么意思
- 奥基夫是什么意思
- 奥妙是什么意思
- 奥妙无穷是什么意思
- 奥委会是什么意思
- 奥威尔是什么意思
- 奥尔是什么意思
- 奥尔夫是什么意思
- 奥尔登是什么意思
- 奥尔良是什么意思
- 奥尼尔是什么意思
- 奥布赖恩是什么意思
- 奥康纳是什么意思
- 奥得河是什么意思
- 奥德修斯是什么意思
- 奥德赛是什么意思